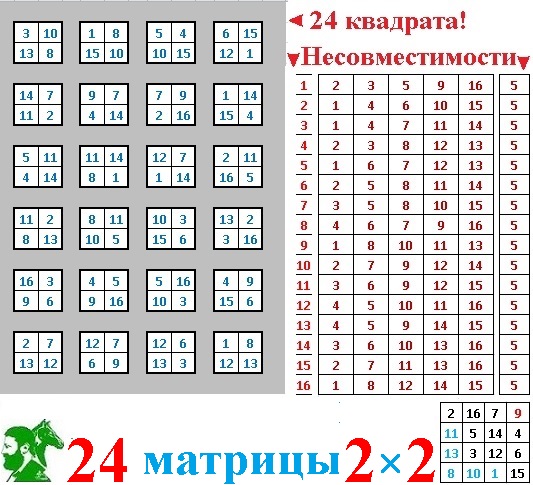
24 матрицы 2х2

Magic! Основа
Алексей Ратушный
Рассмотрим базисную Игру Чисел на примере магического квадрата Surmico.
Как я уже не раз писал, имеется ровно 24 матрицы 2х2 (квадратных таблички из четырёх элементов, со стороной в два квадрата), из комбинаций которых конструируются все 384 совершенных магических квадрата четвёртого порядка, которые дают константу магического квадрата из 40 наборов по четыре элемента в каждом.
Эти двадцать четыре матрицы мой драгоценный Читатель видит на иллюстрации.


Матрица №1
14_____7
11_____2

Матрица №2
5_____11
4_____14

Матрица №3
11_____2
8_____13

Матрица №4
16_____3
9_____6

Матрица №5
2_____7
13_____12

Матрица №6
9_____7
4_____14

Матрица №7
11_____14
8_____1

Матрица №8
8_____11
10_____5

Матрица №9
4_____5
9_____16

Матрица №10
12_____7
6_____9

Матрица №11
7_____9
2_____16

Матрица №12
12_____7
1_____14

Матрица №13
10_____3
15_____6

Матрица №14
5_____16
10_____3

Матрица №15
12_____6
13_____3

Матрица №16
1_____14
15_____4

Матрица №17
2_____11
16_____5

Матрица №18
13_____2
3_____16

Матрица №19
4_____9
15_____6

Матрица №20
1_____8
12_____13

Матрица №21
3_____10
13_____8

Матрица №22
1_____8
15_____10

Матрица №23
5_____4
10_____15

Матрица №24
6_____15
12_____1

Нумерация матриц в этой публикации произвольная.
Просто для удобства фиксации.

Легко убедиться, что далеко не все числа любят соседствовать на этих воистину волшебных квадратиках.

Рядом с изображениями матриц на иллюстрации мой любимый Читатель обнаруживает табличку «несходимостей» Чисел друг с другом.
Для каждого из 16-ти Чисел указаны пять других Чисел, с которыми это Число «не дружит».

О, сколько нам видений чудных готовит рассматривание этого Чуда света!
И о каждом мы надеемся еще пообщаться с Читателем!