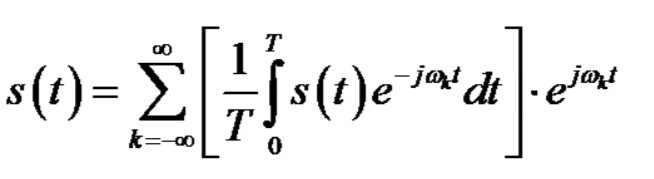Двадцать седьмой этаж математики

Интегральные преобразования, специальные функции, теория групп, группы Ли, математические модели нелинейной динамики etc в здесь и сейчас, в текущей и глобальной перспективе.

В современном мире, где наука и технологии стремительно развиваются, интегральные преобразования и специальные функции становятся не просто абстрактными математическими инструментами, а ключевыми элементами в решении реальных задач. Давайте разберёмся, как эти концепты переплетаются с теорией групп, включая группы Ли, и как они влияют на математические модели нелинейной динамики.

Интегральные преобразования и специальные функции

Интегральные преобразования, такие как преобразование Фурье и Лапласа, играют центральную роль в анализе сигналов и систем. Они позволяют переводить временные ряды в частотную область, что критически важно для обработки данных в реальном времени — от обработки изображений до анализа финансовых рынков. Специальные функции, такие как функции Бесселя и функции Гаусса, часто возникают в решениях дифференциальных уравнений, описывающих физические явления — от квантовой механики до теории поля.

Теория групп и группы Ли

Теория групп предоставляет мощный язык для описания симметрий в физических системах. Группы Ли, в частности, являются непрерывными группами симметрий, которые находят применение в квантовой механике и теории относительности. Они позволяют формализовать понятия, связанные с преобразованиями пространства и времени, что открывает двери для понимания фундаментальных взаимодействий в природе.

Нелинейная динамика

Нелинейная динамика — это область математики и физики, изучающая системы, поведение которых не подчиняется принципам суперпозиции. Математические модели нелинейной динамики применяются в самых разных сферах: от метеорологии до биологии. Например, уравнения Навье-Стокса описывают движение жидкости и газа, а их решения могут быть крайне чувствительны к начальным условиям, что приводит к феноменам хаоса.

Здесь и сейчас: глобальная перспектива

В текущей глобальной перспективе интегральные преобразования и специальные функции становятся особенно актуальными в контексте больших данных и машинного обучения. Методы анализа данных используют эти математические инструменты для извлечения информации из огромных массивов данных. Теория групп также находит свое применение в квантовых вычислениях, где симметрии играют ключевую роль в оптимизации алгоритмов.

Заключение

Таким образом, интегральные преобразования, специальные функции, теория групп и нелинейная динамика — это не просто абстракции. Это инструменты, которые помогают нам понимать и моделировать сложные системы в нашем мире. Их актуальность только возрастает с развитием технологий и научных исследований. Важно помнить, что за каждым математическим понятием стоят реальные процессы и явления, которые формируют наше восприятие мира. В этом контексте математика становится не просто языком науки, а универсальным инструментом для исследования самой сути нашего существования.