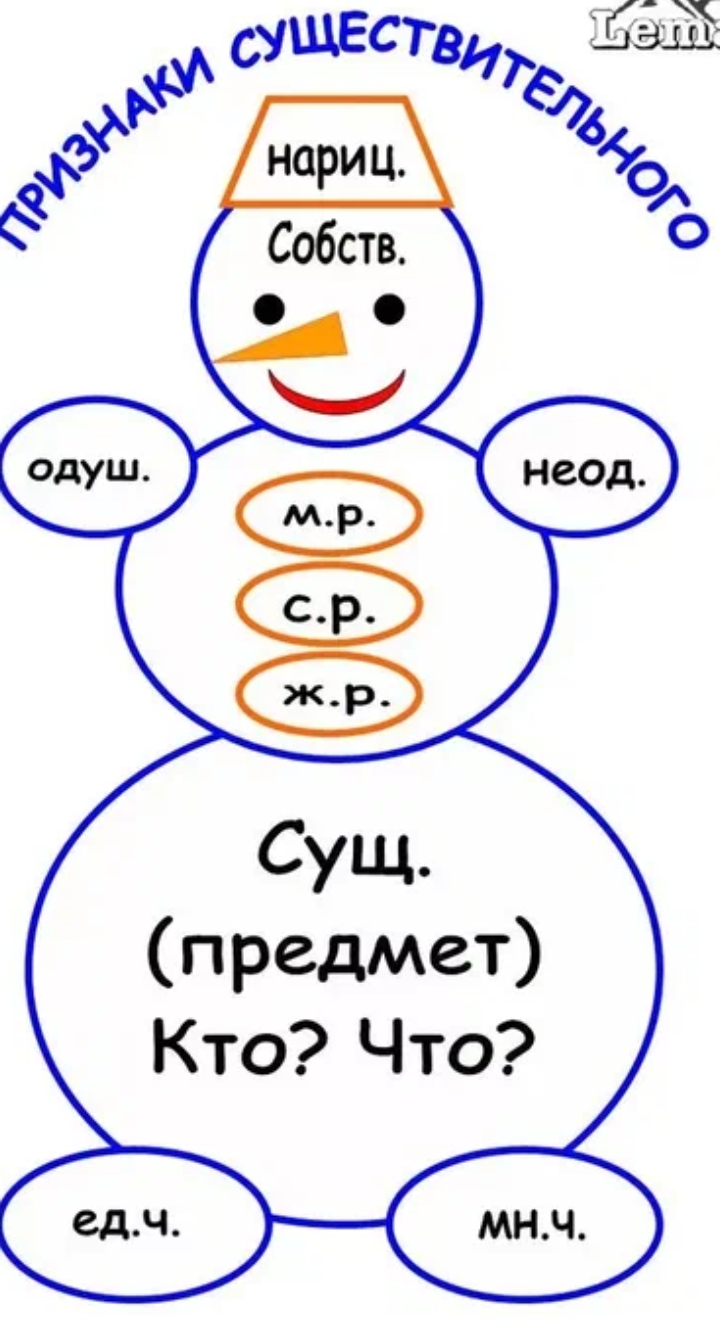
Существительное - существует,

 прилагательное- прилагает, производная - производит, а предел? - вот в чём собака зарыта.

Существительное называет предметы в широком смысле слова; это — названия вещей (стол, стена, окно, ножницы, сани), лиц (ребёнок, девочка, юноша, женщина, человек), веществ (крупа, мука, сахар, сливки, кислота), живых существ и организмов (кошка, собака, ворона, дятел, змея, окунь, щука, бактерия, вирус, микроб), фактов, событий, явлений (пожар, спектакль, беседа, каникулы, печаль, страх, радость), географические положения (Россия, Байкал, Оренбург, Европа, Азия), а также качеств, свойств, действий, состояний (доброта, глупость, синева, бег, решение, толкотня).

Прилага;тельное — самостоятельная часть речи, обозначающая непроцессуальный признак предмета и отвечающая на вопросы «какой?», «какая?», «какое?», «какие?», «чей?» и так далее. В русском языке прилагательные изменяются по родам, падежам и числам, могут иметь краткую форму. В предложении прилагательное чаще всего бывает определением, но может быть и сказуемым. Имеет тот же падеж, что и имя существительное, к которому оно относится.

Производная - это математическая операция, которая позволяет определить скорость изменения функции в каждой точке ее области определения. В контексте Монте-Карло, производная используется для нахождения приближенного значения интеграла функции, которая не может быть проинтегрирована аналитически. Для этого используется метод Монте-Карло численного интегрирования, который основан на генерации случайных чисел и оценке интеграла на основе этих чисел. Приближенное значение интеграла вычисляется путем усреднения значений функции в случайно выбранных точках области интегрирования. Производная функции в каждой точке вычисляется как предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю.

Предел - это математический объект, который определяет поведение функции вблизи некоторой точки. Формально, предел функции f(x) при x, стремящемся к a, равен L, если для любого положительного числа ; существует положительное число ; такое, что для всех x, удовлетворяющих условию 0 < |x - a| < ;, выполняется неравенство |f(x) - L| < ;. Иными словами, если мы можем выбрать сколь угодно малое окрестность точки a, то мы можем найти такое значение функции L, что все значения функции в этой окрестности будут находиться на расстоянии меньше ; от L. Пределы используются в математике для определения непрерывности функций, вычисления производных и интегралов, а также в других областях, связанных с анализом функций и их свойствами.

Повторение - мать, отец, дед, бабушка и.... все предки вплоть до пращура Луки учения.

Успехов и процветания!