Принцип наименьшего действия

ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ
И ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ


Природа ничего не делает напрасно и во всех своих проявлениях избирает кратчайший или легчайший путь.
    - Аристотель

Природа всегда действует наиболее короткими путями. 
   - Пьер Ферма

Столько лени накопилось хоть с дивана не вставай,
   - В. Поляков

Кратчайший путь берёт луч света
От точи А до точки Б.
Как узнаёт его? Об этом
Мы поведём рассказ в стихе.

Природа следует законам,
Что эффективны и просты -
Кратчайший путь, ведущий к дому,
Примером этой красоты.

Другим примером - энтропия,
Чтоб максимальная была.
Энергии минимум стихия
Чтобы система отдала.

Когда вам очень интересно
Найти какой-нибудь экстрим
Где максимум чего-то местный
Иль минимум найти хотим.

Вот эта область и зовётся
Как “вариации задач”.
Её не учит кто придётся,
У многих вызывала плач.

Природа этот принцип знает
И следует ему во всём -
Усилия меньше применяет -
Мы путь короче не найдём.

Так все законы сохранения
И преломления луча
Без вариаций вычисления
Нам не найти, попытки - зря.

Заметил Аристотель это,
Ферма научно подтвердил,
Дал метод Эйлер одним летом,
Лагранж формально утвердил.

Теперь механика движения
И свойства квантовых полей
Используют эти уравнения!
Природе и без них видней.


Иллюстрация:

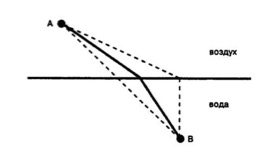
Принцип Ферма (принцип наименьшего времени Ферма - 1662 г.) — постулат в геометрической оптике, согласно которому свет выбирает из множества путей между двумя точками тот путь, который потребует наименьшего времени.


Принцип наименьшего действия (ПНД) утверждает:
система ведёт себя таким образом, чтобы ее «действие» было минимальным (или максимальным) из всех возможных при данных условиях.

"Многие законы механики и физики сводятся к утверждению, что некоторый функционал в рассматриваемом процессе должен достигать минимума или максимума. В такой формулировке эти законы носят название вариационных принципов механики или физики.
К числу таких вариационных принципов или простейших следствий из них принадлежат: принцип наименьшего действия, закон сохранения энергии, закон сохранения импульса, закон сохранения количества движения, закон сохранения момента количества движения, различные вариационные принципы классической и релятивистской теории поля, принцип Ферма в оптике,  т.д."
          - Эльсгольц Л.Э


8-9-21


БРАХИСТОХРОНА ИЛИ ЛЬВА УЗНАЮТ ПО КОГТЯМ

Брахистохро;на (от греч. «кратчайший» + «время») — кривая скорейшего спуска.

«По когтям узнают льва».
         - И. Бернулли


Всегда в науке было модно
Загнать товарищей тупик
Задачей иль идеей сложной,
С вопросом новым, что возник.

Брахисто-хрона, - не годится
Для рифмы греческой в звено:
“Как шарику с вершин скатиться,
Чтоб время - минимум его”.

Условие просто , ну, как репа,
Задал Бернулли, сам саван.
Четыре получил ответа,
Один без подписи был дан.

По элегантности решения,
Его особой глубине,
Был узнан автор вне сомнения,
Бернулли там сказал о льве


В 1696 году двадцатидевятилетний Иоганн Бернулли выдвинул задачу, которой было суждено сыграть выдающуюся роль в развитии одной из важнейших ветвей математического анализа.
Она была удивительно проста на первый взгляд, эта задача.

ВОПРОС:
Требовалось найти кривую, при движении по которой под действием силы тяжести, шарик пройдет путь из точки A в точку B за наименьшее время. 

Было получено четыре решения (Лейбниц, Я. Бернулли, автор задачи, И Бернулли)  и  было прислано решение анонимного автора. Увидев  решение этой задачи, содержавшее всего 77 слов, И. Бернулли угадал автора И. Ньютона — «По когтям узнают льва».


ОТВЕТ:
Быстрее всего шарик скатится по линии «кратчайшего времени» — брахистохроне.
В данном случае ею служит циклоида с горизонтальным основанием и точкой возврата в начальную точку А.


Задача о брахистохроне, послужила толчком для развития вариационного исчисления — одного из самых могущественных инструментов в руках современных физиков и механиков.

4-10-23