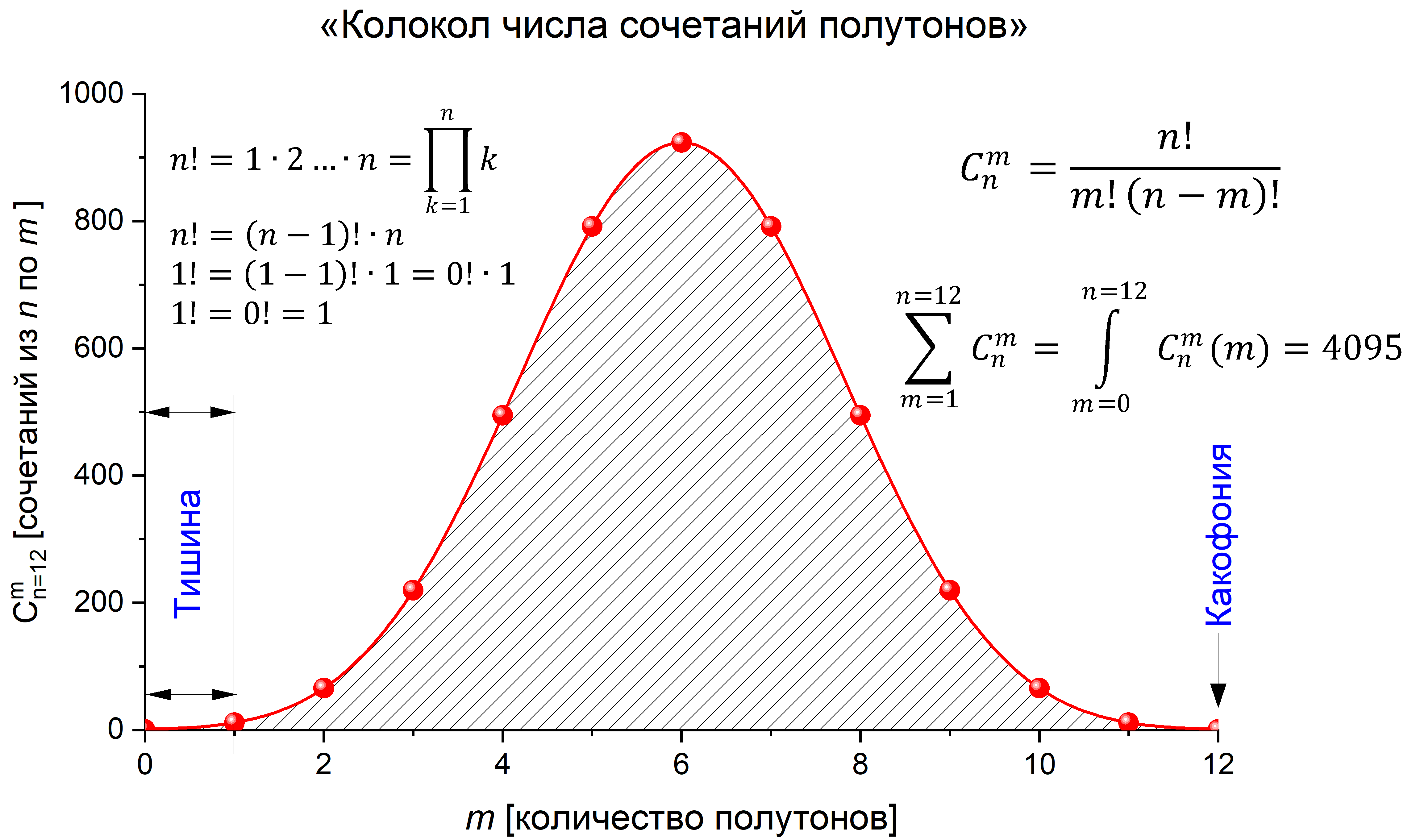
Колокол сочетаний

Прежде чем мы установим общее количество и состав всех аккордов, возможных
в музыкальном звукоряде из 12 полутонов, подсчитаем общее количество всех
уникальных сочетаний из n=12 по m=1...12 элементов.

Для этого воспользуемся изящной формулой, известной нам ещё из школьного курса
комбинаторики, электронными таблицами Excel, в которых имеется встроенная функция
ФАКТР(n) для подсчёта факториалов вида n!=1*2*3...*n, а также программой Origin,
предназначенной для построения графиков и численного анализа данных.

Очень скоро мы увидим, что общее количество уникальных сочетаний составляет 4095:

m      Cочетаний (из n=12 по m)
1           12
2           66
3           220
4           495
5           792
6           924
7           792
8           495
9           220
10           66
11           12
12           1
Всего:  4095

А поскольку нам сразу бросится в глаза, что количество сочетаний проходит через
максимум C(n,m)=924 при m=6, а остальные C(n,m) симметричны относительно него,
то мы захотим построить зависимость количества сочетаний от числа звуков в них.

Полученная кривая будет очень похожа на колоколообразную кривую Гаусса, а площадь
под ней (после добавления точки m=0, C(n,m)=1) удивительным образом совпадёт с
суммой 4095. Что же означает добавление нулевой точки?.. – Тишину!

Это тот случай, когда при подсчёте количества сочетаний не задействован ни один
из 12 полутонов нашего музыкального звукоряда, независимо от числа октав в нём.

Это значит, что тишина является антиподом какофонического звучания всех 12-ти
полутонов. В обоих случаях (тишины и какофонии) число сочетаний равно единице:
C(12,12) = C(12,0) = 1. Это связано с тем, что 0! (ноль-факториал), который
используется при подсчёте числа сочетаний C(12,0) (из 12-ти по 0), равен 1.

Итак, наивысшей гармонией обладает тишина – сочетание нуля из 12 полутонов.
Возможно, это связано ещё и с тем, что её "зона обитания" не ограничивается нулём
звуков, но простирается от нуля до ОДНОГО полутона, при том, что количество
полутонов не бывает дробным, как количество клавиш на фортепиано.

Будучи пустым множеством (с точки зрения количества полутонов в ней), тишина,
тем не менее, не пуста (с точки зрения количества множеств, равного единице).
А поскольку C(12,0)=C(12,12)=1, это объясняет, почему она всегда звучит на одной
ноте, которая соответствует анти-какофонии, то есть абсолютной гармонии.

Если одновременно сыграть все возможные музыкальные произведения прошлого,
настоящего и будущего, то получим абсолютную какофонию. Если же их всех
одновременно промолчать, то получим серебристое звучание тишины.

(2022)