Математика. ЕГЭ. Стереометрические построения

   
  Речь пойдёт о стереометрии для математиков
  Уточню - для будущих математиков.
  Речь идёт о некой программе, направленной на подготовку к ЕГЭ по части всяких геометрических построений, и помогающей зрительно представить чертёж, связанный с решением поставленного задания.

  Задания по стереометрии берутся из туров ЕГЭ прошедших годов, а роль преподавателя состоит в том, чтобы построить самому, или помочь построить ученикам, соответствующий заданию чертёж в изометрии.
  На втором этапе предлагается сделать на чертеже дополнительные построения и, тем самым, решить задачу. Разумеется, тому, кто не справится, можно предложить и решение - итоговый чертёж с поясняющим текстом.

  Такая программа, как мне кажется, будет востребована, а по части красот программирования она оказалась весьма привлекательной для меня.
  Поэтому я сообщаю, что заканчиваю публикацию статей по теме редактора для художественного рисования и открываю новый проект, с пространственной векторной графикой.
  Этот проект к настоящему времени я уже достаточно продвинул, и пришло время писать статьи. С тем, чтобы, во-первых, не позабыть некоторые подробности, а, во-вторых, чтобы поделиться своим опытом с вами, уважаемые читатели.

   ЧТО ИМЕЕТСЯ В ИНТЕРНЕТЕ

   Программы, натаскивающие учеников к ЕГЭ, имеются в интернете. По части стереометрии интересен онлайн сервис под названием Лаборатория «Стереометрия» https://clck.ru/Ys7XD со своими собственными простенькими заданиями. Однако для серьёзной подготовки к ЕГЭ он не очень годится.
   Разработчики сервиса, конечно, постарались, но влезть в него со стороны с тем, чтобы поставить свои собственные задачи – это непонятно как делать. Я же хочу сделать программу, удобную и в этом плане.

   ИНТЕРФЕЙС

  Значительную часть интерфейса я позаимствовал из программы для художественного рисования. Работа с полями, чтение и запись картинки во внешние файлы, перемещение поля для рисования с помощью стрелочек – все эти удобства я сохранил в новом проекте. Сокращена палитра выбора цвета, но оставлены кнопочки темнения и светления тона. Ластик перекочевал в нижнюю часть левой панели.

  На освободившуюся часть левой панели помещены кнопки управления векторной графикой, а ниже этих кнопок имеется панель инструментов, и кнопки выбора.

  СТРУКТУРА ГРАФИКИ

  Структуру графики я тоже заимствовал из программы для художественного рисования. Графические элементы, такие, как точки, прямые, отрезки, плоскости и сечения, представляются в форме строк из целых чисел.
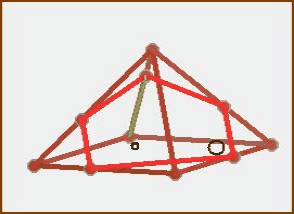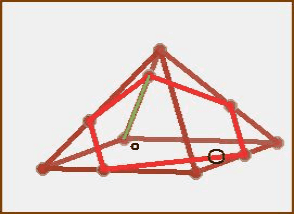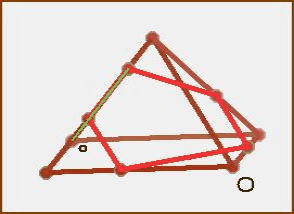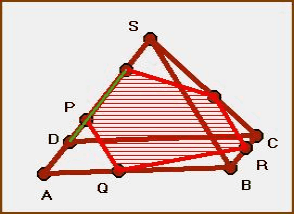
  К примеру, точка «R», которую вы видите нарисованной на чертеже, представляется строкой –

16>     1  2953  2081  0  0  0  0  7  0  30802  148  5  16

1 здесь логотип точки,
2953, 2081, 0 – координаты X,Y,Z увеличенные в 10 раз,
7 – привязка к седьмому отрезку, на котором точка находится, нужна ли эта привязка, я пока не решил.
148 – цвет точки, 5 – её размер, 8 – её уникальный номер (1-255)

Число 30802 это буквенное обозначение точки. Число это содержит код символа, обозначающего латинскую букву, индекс 1-5 или ноль, как маленькая буква «о», следующие за латинской буквой, а также позицию – место расположения буквенного обозначения.
  Позиция – это число от нуля до 15. Это то место, на котором будет напечатана буква.

  ОФОРМЛЕНИЕ ЗАДАНИЯ

Задание, вместе с графической иллюстрацией к нему, может быть помещено в обычный текстовый файл. Выглядит этот файл, например, так –

Задание 1.
В правильной треугольной пирамиде SABC сторона основания AB равна 9, а боковое ребро SA=6. На рёбрах AB и SC отмечены точки K и M соответственно, причём AK : KB = SM : MC=2:7. Плоскость а содержит прямую KM и параллельна прямой SA.
 а) Докажите, что плоскость а делит ребро SB в отношении 2 : 7, считая от вершины S.
 б) Найдите расстояние между прямыми SA и KM.

X  просмотр__ 1-точка 2-отрезок 3-прямая 4-плоскость 5-сечение N_строк= 8
_____    x= 100  y= 400  u= 30  k= 40

    1>    2 -176  481  0  4245 -948  0  0  0  20546  2326  5  1
    2>    2  3273  3596  0 -176  481  0  0  0  2115   2326  5  2
    3>    2  4245 -948  0  3273  3596  0  0  0  12353  2326  5  3
    4>    2  3273  3596  0  2448  1043  1549  0  0  4179  2326  5  4
    5>    2  3488  2585  0  1864  917  1206  0  0  77  31008  5  5
    6>    2 -176  481  0  2448  1043  1549  0  0  0  2326  5  6
    7>    2  4245 -948  0  2448  1043  1549  0  0  0  2326  5  7
    8>    1  3488  2587  0  0  0  0  3  0  20555  2326  5  8


  Естественно, графическое приложение к заданию не делается вручную. Программа имеет средства для создания чертежа с помощью своих инструментов.


    ВРАЩЕНИЕ МОДЕЛИ

       Режим поворота модели активируется кликом по голубому
  полю с изображением координатных осей. На белом поле выше показываются
  характеристики системы. В программе принята фронтально косоугольная
  система, её характеристики могут выглядеть, например, так -
         x100y400u30k.4
  что означает - начало координат находится на 100 пикселей правее левой
  кромки рисунка и на 400 пикселей ниже верхнего его края. Ось Y составляет
  угол 30 градусов с осью X и сокращена в линейных размерах на величину k=.4
    Если Вас эти цифры почему либо не устраивают, то Вы исправляете их на
  белом поле и запоминаете их, вторично кликнув по голубому полю и выйдя из
  режима поворота.
 
    Собственно вращение делается так - в основании модели кликом правой
  кнопки мыши намечаем вертикальную ось поворота. В этой точке появляется
  маленький кружок. А правее его - большой кружок. Двигая большой кружок
  мы и проводим вращение.
    В процессе вращения появляется воздушная перспектива. Силу перспективы
  можно регулировать, используя Ластик разных цветов. Кнопка «cls»
  возвращает модель в исходное состояние. Кнопка «ok» закрепляет модель
  в том положении, в которое мы её повернули.

  Описанный поворот модели демонстрируется на гифке - на иллюстрации к этой статье. Такое наглядное пространственное изображение модели с возможностью её поворота и увеличения, очень удобно.
  Тот, кто хочет познакомиться с программой и поработать с ней, может скачать её отсюда - http://disk.yandex.ru/d/T5-M4ZNJabZ9yw Программа работает в среде Виндос.