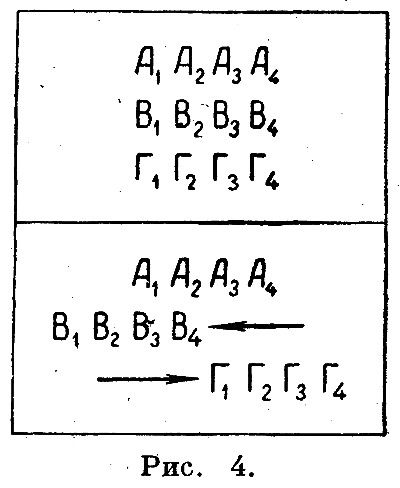
Итоги. Апория Стадион 2

       Но, может быть, кому-то всё ещё непонятно как я получаю не только зеноновские 2 равно 4 или половина равна целому, а и другие числа - 0 или 3. Ради бога, поэкспериментируем ещё и пока для максимальной простоты с двумя противоположно движущимися рядами.
      Мы брали первых бегунов левой группы и правой группы, которые в начале движения стояли "точка в точку". Естественно, что в результате мы получили 4 единицы расстояния между ними, потому что один прошёл 2 единицы от "нуля" и второй прошёл 2 единицы от нуля в противоположную сторону.
     Возьмём теперь вторых бегунов - второго из левого ряда и второго из правого ряда. "Вторые" бегуны в начале отстоят друг от друга на расстоянии 2 единицы. А после того, как предложенное движение совершится (т.е. когда каждый из бегунов сущностно пройдёт свои собственные две единицы расстояния), они снова окажутся друг от друга на расстоянии в 2 единицы. Следовательно по зеноновской логике 4 будет равно 2 и равно 0.
     То есть 4 "первых" бегунов равно 2 сущностного движения любого бегуна и равно 0 "вторых" бегунов (расстояние между ними было 2 единицы и осталось 2 единицы, значит путь равен 0). Конечно, это 2 единицы будут в разные стороны, и "второй" бегун, который был слева станет справа, а "второй", который был справа станет слева, но Зенон то ни на что из этого не обращает внимания.
    Можно получить и другие числа, и 3, о которых мы писали, и 5 и т.д.
Возьмём просто несколько иную схему. Пока наша схема была условной, ориентировочной. Но теперь, понимая что происходит с нашей "путаницей", мы можем уже не просто предположить, а точно выявить именно зеноновскую схему.
Сейчас мы покажем какой была именно зеноновская схема и почему по нашему убеждению она была именно такой. Итак, берём некоторую вторую схему, отличающуюся от первой.
    Пусть стадион состоит ровно из 7 единиц расстояния, или из 7 стадий. Первый неподвижный ряд бегунов застывает посредине этого стадиона - на 2 стадии от левого края и на 2 стадии от правого края, в себе он содержит 3 стадии между 4 бегунами. Таким образом он как бы уравновешен посередине. Тогда левые бегуны, выстроенные от левого края заполняют 2 свободные левые стадии и перекрывают 1 стадию бегунов неподвижных, серединных. Правые точно также аналогично с правого борта. И тогда первый бегун слева и первый бегун справа стоят не в одной точке, как было по Аристотелю и как мы приняли для начала вслед за ним, а на расстоянии в 1 стадию друг от друга.
    Зачем нужно именно такое построение и почему я думаю, что через это мы сможем выявить какая всё-таки схема была у Зенона? Пока скажем так - затем, что это внешним образом красиво. Ведь после того, как каждый бегун левого и правого ряда пройдёт по 2 положенные ему стадии, все три группы застынут ровно одна против другой, и к тому же ещё и ровно посередине стадиона. И можно предположить что тот, кого называли "Паламед элейский", то есть явно любящий покрасоваться, должен был придумать нечто именно такое - не любой типичный вариант, а самый "завлекательный", "удобный", "шокирующий", "показательный". И хотя не все признают подобные причины причинами, я думаю, что порой это одни из главных причин (в случае Зенона уж точно).
     К тому же, помимо красоты есть и другая польза именно от такого варианта - наглядность.
     На фоне неподвижных бегунов мы зримо можем увидеть как, допустим, первый левый бегун проходит до конца неподвижных бегунов положенные ему 2 стадии, и при этом также зримо можем увидеть, что первый правый бегун в это время окажется на противоположном конце.
     Однако, при всей наглядности и красоте, будет ли работать данная схема на руку Зенону?
     Когда первые левые и правые бегуны пройдут по 2 свои стадии, они окажутся в конце и в начале неподвижной группы - каково же расстояние между концом и началом неподвижной группы? Это расстояние в 3 стадии. Итак, вот оно наше 3, которое тоже равно 2, но это не зеноновский вариант, ибо Зенон предпочитал не показывать до конца дурноту "всё равно всему", чтобы не намекнуть тем самым никому случайно какой тут вообще возможен бардак при смешении сущностного движения с любым относительным.
     А теперь посмотрим, что мы будем получать, если бегуны пройдут только 1 стадию. Тогда, очевидно, первый левый переместится на прежнее место первого правого, а первый правый на прежнее место первого левого, и мы получим, что расстояние между ними останется ровно тем же, что и было. То есть окажется, что эти бегуны не перемещались, хотя они перемещались, и что 1 равно 0. Думаю, все остальные варианты мы рассматривать уже не будем, ведь совершенно понятно, что можно получить любое число равное любому числу в зависимости от расстановки.
Но в чём мы убедились точно, так это в том, что вариант Зенона, озвученный по иному, был всё-таки Аристотелевским, ибо только тогда, когда первые бегуны справа и слева в одной точке в начале, они проходят, проходя 2 стадии, - 4. И если мы в Аристотелевском варианте посмотрим что будет при прохождении бегунами 1 стадии, то увидим, что в результате между ними будет 2 стадии и тогда совершенно чётко можно будет сказать то, что и говорил Зенон - 2 равно 1, или в пересчёте на время - целое время, потраченное на 2 стадии равно половине времени, потраченного на 1 стадию.
     Так что Аристотель ближе всего передал вариант Зенона.
   Но наши добавочные варианты были не бесполезны и хорошо показали общий фон полной относительности.
    А теперь вернёмся к опровержению. Поскольку и его могли усвоить и понять не до конца, попробуем предложить ещё одну аналогичную картинку для понимания.
Все мы неплохо разбираемся в практических делах, вот и давайте возьмём определённую практическую ситуацию.
     Допустим есть предприниматель, хозяин, и ему нужно произвести товар. Он берёт к себе двух одинаковых работников, работающих с равной скоростью и качеством. За 1 час времени 1 работник производит 1 товар. И вот, наш хозяин, наш предприниматель, аналогично бегунам на стадионе, даёт своим работникам 2 часа времени. Естественно, за это время работники произведут 4 товара. И вот теперь спрашивается - сколько же времени мы имеем? Ведь предприниматель достал часы и на них прошло ровно 2 часа. Значит мы имеем 2 часа времени? Однако, если мы посмотрим на наши товары, то в них заключено вовсе не 2 часа времени, а 4 часа. И тогда получается всё, как у Зенона - что 2 часа времени равно 4. Причём этот факт открыто признаёт сам хозяин - он приходит и платит одному работнику за 2 часа времени труда и второму за 2 часа времени труда. Вот вам "марксистский" парадокс времени на зеноновской основе. Но что не хочет понять Зенон так это то, что если бы работников было 6, то 2 часа равнялись бы уже 12, и что так происходит всегда там, где мы ведём речь об относительности. Относительно количества работников сущностное время превращается в неопределённую величину - в одни и те же 2 часа может влезть 1000 или 100000 относительных рабочих часов.
Поэтому Декарт говорит, допустим про первый вариант из 2 рабочих - относительное время в 4 часа состоит из 2 часов первого рабочего и 2 часов второго рабочего, но поскольку это время действительно относительно, то капиталисту всё равно и мы можем предположить, что эти 4 часа или 4 товара произвёл только один из рабочих, а второй валялся и спал - в общем работал либо первый, либо второй. Главное, что 4 товара у нас в конце.
     Но, как вы думаете, ошибётся ли капиталист и продаст ли он произведённые товары как заключающие лишь 2 часа времени? Нет, конечно же, продаст как 4 (остальные надбавки пока не учитываем). Он не ошибётся в сущностном и относительном, хотя и не изучал философии. Поэтому капиталисты в своей эмпирии не ошибаются, почему же ошибаемся мы вслед за Зеноном? Почему мы не можем прямо сказать, что хотя у нас прошло 2 часа времени, но у нас было и 2 работника, и поэтому имеем в результате, в наличии - 4 часа. И аналогично, хотя каждый отдельный бегун пробежал две стадии, но у нас было два бегуна. движущихся в противоположном направлении, и поэтому в результате - в относительной картине мира мы имеем 4 стадии пройденного пути???

     И наконец, последнее. На тот случай, если мне вдруг скажут, некоторые умники, что я неправильно считаю. Мол, в красивом варианте, когда первые бегуны отстоят друг от друга на 1 стадию и когда закончив движение, будут отстоять друг от друга на 3 стадии, то неправильно считать, что 2 будет равно 3, потому что относительное движение первых бегунов будет 1 пройденная стадия друг до друга и плюс ещё 3 после, и того снова 4, как у Зенона. Но, дорогие мои, что же вы тогда считаете? Вы же тогда в точности считаете расстояние, пройденное 1 бегуном плюс расстояние, пройденное другим бегуном, и как говорится, на здоровье, но зачем же при этом тут же забывать, что бегунов 2 и приравнивать путь 1 бегуна к пути 2-х?
     Зенон, он же решил над нами подшутить, просто складывая суммы работников-бегунов и приравнивая их одному работнику. В общем, на марксистском языке приравнял производительность труда количеству произведённого.
     Так что если хотите - считайте следом за Зеноном, но всё равно казус.
А я считаю то, что и представляет из себя в действительности относительность - результат. Если бегуны отстояли друг от друга на 1 стадию и прошли оба по 1 стадии и снова отстоят друг от друга на 1 стадию, то относительности движения всё равно кто там был слева, а кто справа - отрезок между телами был равен 1 и остался равен 1, значит пройденное расстояние - 0. И вообще, совершенно неважно тут как считать, неважно брать ли бегунов, как я взяла их - точно колышки, когда их 4, а стадий между ними 3, как между 4-мя колышками; или же брать 4 равных тела, каждое длиной по стадию и тогда на 4 тела приходилось бы и 4 стадии.
Не это важно в апории Зенона.
     В ней важно то, что относительность рассматриваемого движения позволяет нам или вполне допускает приписывать одному телу - движение сразу же двух тел, или даже большего количества тел. Позволяет перелить общее относительное движение в одну сторону. И в этом заключается вся апория Зенона - сущностное движение одного тела приравнивается в ней относительному движению многих тел, перелитых в это одно.

     Опасность относительного уровня рассмотрения движения заключается в том, что тело вообще может не двигаться, а ему при этом можно приписать какое угодно движение, если другое тело к которому мы его относим полетело от него в какую-то сторону, и при этом мы решили считать летящее - покоящимся, а наше двигающимся. Поэтому 0 или действительный покой нашего тела в призме относительности может быть равен 1, 2, 3, 4 - в принципе чему-угодно, и данный случай апории, выхваченный из этого релятивного подхода Зеноном, когда 2 равно 4 или 1 равен 2 или половина равна целому - есть лишь его частный случай, только один из бесконечно многих.