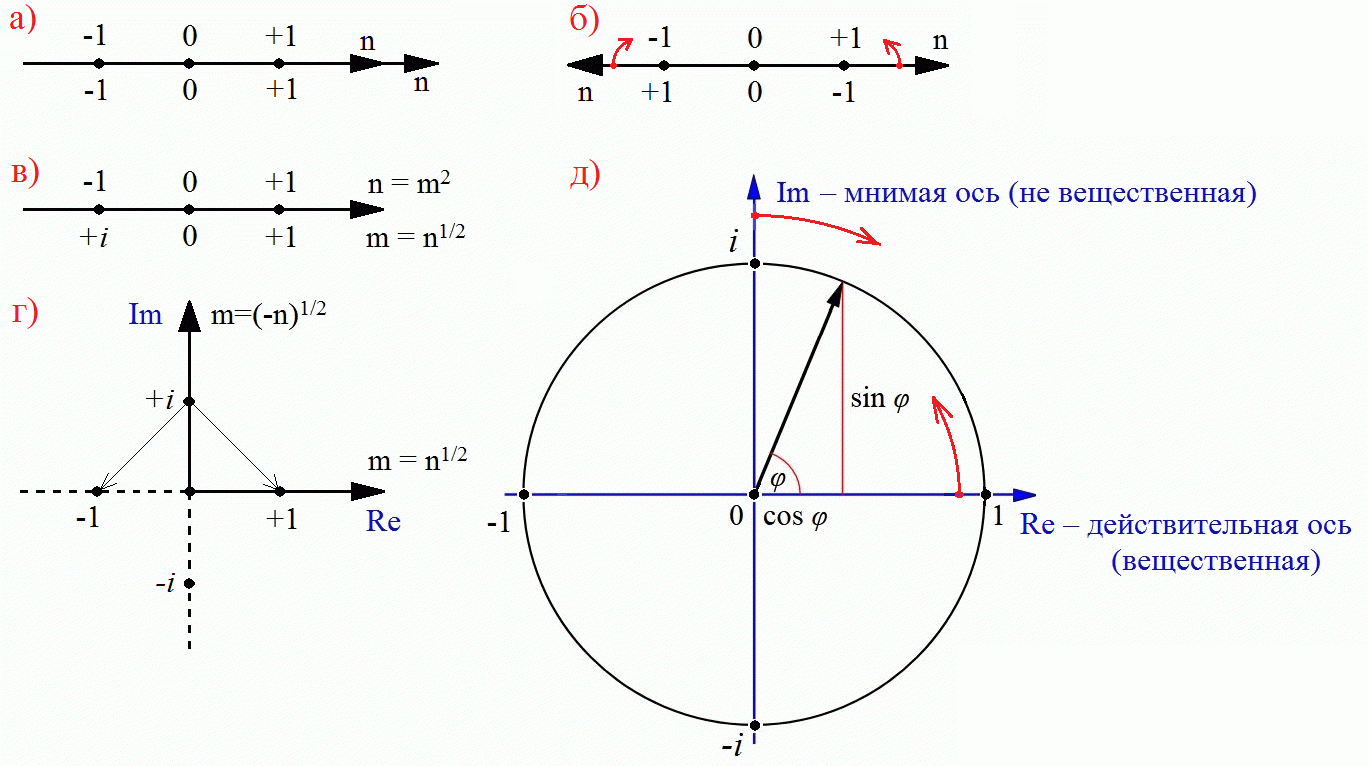
Диполь мнимой единицы

1. Комплексная плоскость (m)*(m*i) образуется пересечением под прямым углом
действительной (m) и мнимой (m*i) осей. Точка их пересечения называется нулевым
началом координат и обозначается цифрой 0. Листочек в клеточку является наглядной
моделью такой плоскости, стоит только отметить на нём 0 и провести через него две
взаимно перпендикулярные оси – действительную и мнимую.

Мнимая ось (m*i) отличается от действительной оси (m) лишь наличием множителя i,
который называется мнимой единицей (от латинского слова imaginarius – кажущийся,
призрачный, воображаемый, мнимый). Мнимая единица определяется, как "квадратный
корень из минус единицы", откуда:

                i*i = i^2 = -1                (1)

Из равенства площадей квадратов (i*i)=(-1*1)=(-1) следует, что:

                i=-+1                (2)

То есть, мнимая единица одновременно равна минус единице и плюс единице.
Это единственная причина, по которой её невозможно представить в виде точки на
действительной числовой оси. Но в виде пары чисел: +1 и -1, образующих числовой
диполь ("двухполюсник") i=-+1 её представить нетрудно.

2. Пусть действительная (m) и мнимая (m*i) оси могут свободно вращаться навстречу
друг другу вокруг общего начала координат 0, как два соосных пропеллера.

Тогда выражение (2) можно трактовать, как варианты совмещения мнимой единицы i
с действительными единицами +1 и -1 на оси (m) в моменты совмещения мнимой и
действительной осей в процессе их встречного вращения.   

Аналогичным образом, существует только два варианта совмещения действительной
единицы 1 с мнимыми единицами +i и -i:

                1=+-i                (3)

что позволяет считать действительные и мнимые числа равными по генезису
(по рождению, происхождению, первородству) и взаимозаменяемыми:
 
                x=+-x*i
                x*i=-+x                (4)

Каждому действительному числу x соответствует пара мнимых чисел (x*i) и (-x*i),
образующих числовой диполь (+-x*i), модуль которого равен модулю действительного
числа x.

Каждому мнимому числу (x*i) соответствует числовой диполь (-+x), состоящий из
двух действительных чисел -x и +x, модули которых равны друг другу и модулю
мнимого числа (x*i).

3. Если заменить мнимую (m*i) и действительную (m) оси, образующие комплексную
плоскость (m)*(m*i), двумя одинаковыми действительными осями (n=m^2), которые
вращаются навстречу друг другу вокруг общего начала координат, то единицы на этих
осях (n) в моменты их совпадения тоже будут совмещаться лишь двумя способами:

(с образованием тождества)    1=1 и -1=-1                (5)

(и с образованием антиномии)  1=-1 и -1=1                (6)

В первом случае (5) действительная плоскость (n*n) выродится в действительную
прямую (n), совпадающую с обеими действительными осями (n), вращающимися
навстречу друг другу.

Во втором случае (6) возникнет числовая ось, НА КОТОРОЙ КАЖДОЕ ПОЛОЖИТЕЛЬНОЕ
ЧИСЛО БУДЕТ РАВНО СВОЕМУ ОТРИЦАТЕЛЬНОМУ ЗНАЧЕНИЮ:

                n=-n                (7)
откуда:
                n/n=-1 или 1=-1                (8)

Если n равно некоторому m^2, то выражение (7) примет вид:

                m^2 = -(m^2)                (9)
Откуда:
                m=m*i                (10)

где i – мнимая единица, равная квадратному корню из минус единицы.

4. Таким образом, мнимые числа вида m*i (а значит, и комплексные числа вида
z=k+m*i, где k и m – действительные числа) обязаны своим происхождением
совмещению двух противоположно направленных действительных числовых осей
(n)=(m^2), которые преобразуются в комплексную плоскость (m)*(m*i) в три этапа,
путём:

1) извлечения квадратного корня из гибридной оси (n=-n), откуда m^2=-m^2;
2) разворотом полученных положительных полупрямых (m) и (m*i) под прямым углом;
3) с последующим прибавлением к ним отрицательных полупрямых -(m) и -(m*i).

Философский смысл мнимой единицы i состоит в признании единства
противоположностей, крайняя форма которого имеет вид антиномии
(противоречия, абсурда): 1=-1 или i=+-1.

Другими словами, мнимая ось (m*i) комплексной плоскости z=k+m*i соответствует тем
явлениям материальной и духовной (материально-духовной) реальности, в которых
противоположности мирно уживаются, например, в электрических диполях или в
"гибельном восторге" Исаака Бабеля и Владимира Высоцкого и т. п.

Что касается действительной оси, то она соответствует борьбе противоположностей,
потому что на ней 1 никогда не равна -1, а те, кто не равны, всегда борются,
хотят они этого, или не хотят. Закон единства и борьбы противоположностей
является синонимом термина "комплексная плоскость".

(2018)