Пятый постулат

Поэты, недопонимая
Евклида пятый постулат,
Всё параллельность судеб мают,
Но в геометрии тупят:
Прямые ПО ОПРЕДЕЛЕНЬЮ,
И в неэвклидовых мирах,
Тогда отменно параллельны,
Лежа не в разных плоскостях,
Коль не имеют общей точки
Пересечения на миг.
Такая точка лишь для случки…
Но если пятый ты постиг,
Тогда по жизни «параллелен»,
Ему согласно, лишь одной,
И в мира метрике уверен,
Бок-о-бок под руку с женой.

Опротестовывая пятый:
По Риману - ты одинок;
По Лобачевскому заклятый
В гареме бесконечном… сдох.

Пятый постулат Евклида, формулировка которого в разных источниках приводится по-разному, с самого начала вызвала спор и желание перевести его в разряд теорем путем построения обоснованного доказательства. Кстати, нередко его подменяют другим выражением, на самом деле придуманным Проклом и известным ещё, как аксиома Плейфера. Оно гласит: НА ПЛОСКОСТИ ЧЕРЕЗ ТОЧКУ, НЕ ПРИНАДЛЕЖАЩЕЙ ДАННОЙ ПРЯМОЙ, ВОЗМОЖНО ПРОВЕСТИ ОДНУ И ТОЛЬКО ОДНУ ПРЯМУЮ, ПАРАЛЛЕЛЬНУЮ ДАННОЙ (это и есть современная формулировка 5-го постулата Евклида).

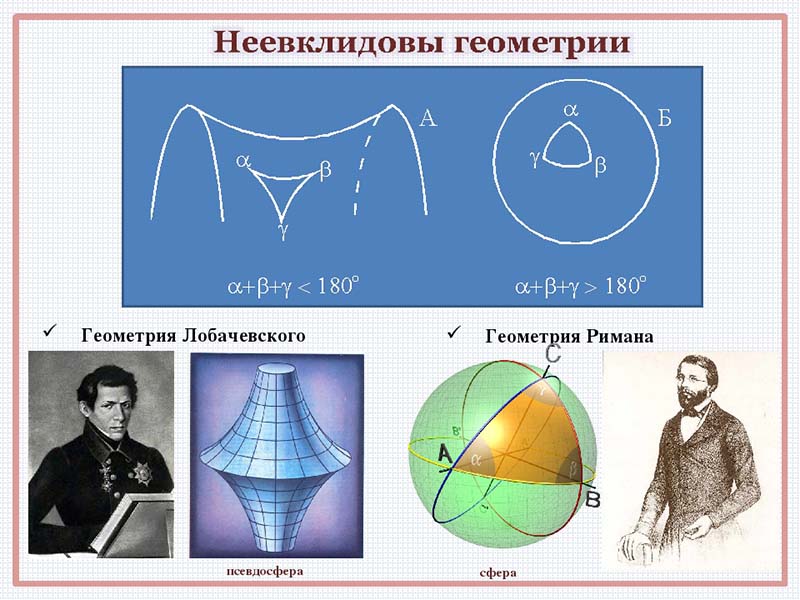
С позиций Римана, который изучал в основном пространства с положительной кривизной, 5-й постулат Евклида звучит достаточно неожиданно. Согласно его идеям, ЧЕРЕЗ ТОЧКУ ВНЕ ДАННОЙ ПРЯМОЙ НЕЛЬЗЯ ПРОВЕСТИ НИ ОДНОЙ ПРЯМОЙ, КОТОРАЯ ПАРАЛЛЕЛЬНА ДАННОЙ.

Лобачевский допускал существование НЕСКОЛЬКИХ (бесконечного числа, согласно современным воззрениям) ПРЯМЫХ, ПАРАЛЛЕЛЬНЫХ ДАННОЙ, И ПРОХОДЯЩИХ ЧЕРЕЗ ТОЧКУ, ЛЕЖАЩУЮ ВНЕ ЭТОЙ ПРЯМОЙ.