Парадокс близнецов в Общей Теории Относительности

Заметка сугубо физическая, хоть и написана предельно популярно.
Только для интересующихся.

Как хорошо известно, «парадокс близнецов» в Специальной Теории Относительности (СТО), никаким парадоксом не является, а лишь неверным распространением принципов СТО на НЕинерциальные системы отсчёта, в то время как в СТО речь идёт об инерциальных и только. Близнец, который совершив полёт к звёздам со скоростью, близкой к скорости света,  и возвратившийся, скажем, через год, обнаружит своего брата близнеца глубоким стариком, ибо на Земле пройдёт не год, а, допустим, много десятилетий. «Парадокс» же заключался, по мнению его авторов, в том, что близнец на Земле считает и себя и улетевшего брата инерциальными системами и потому, с его точки зрения, брат должен был постареть на много-много лет! Но брат путешественник сначала ускорялся, затем замедлял своё движение или двигался по некой кривой, дабы вернуться на Землю. То есть он был явно НЕинерциальной системой отсчёта, такой, что в ней НЕ соблюдаются все законы Ньютона. Он же испытывал силы ускорения -- торможения, центростремительное ускорение и никак не был системой инерциальной.
 
Мы рассмотрим случай «парадокса близнецов» в Общей Теории Относительности.
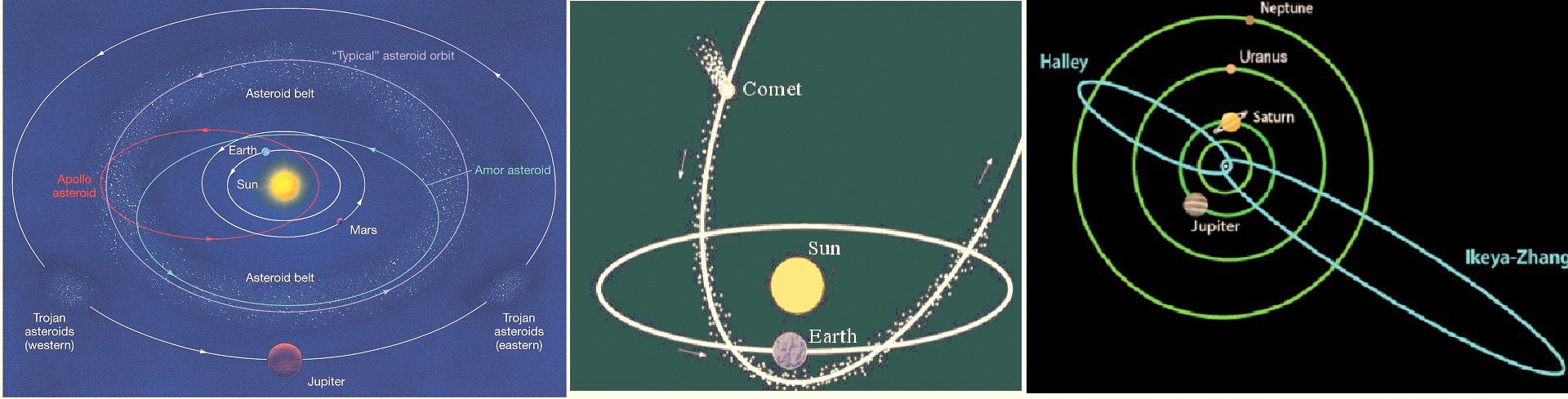
Представим себе некую планетную систему, хотя бы солнечную, в которой вокруг Солнца по эллипсам с малым эксцентриситетом вращаются  планеты. Представим себе также, что в этой системе имеются астероиды и кометы, движущиеся по очень вытянутым эллипсам (с большим эксцентриситетом) вокруг светила.
Допустим, что в некий момент одна из таких комет оказалась поблизости с планетой, имея скорость практически равную планетной.  С планеты на эту комету «перепрыгнул» один из близнецов и затем братья на комете и планете сверили свои часы.
Комета умчалась дальше, а планета продолжала своё движение вокруг Солнца. Через некоторое время, комета, описав некоторое количество эллиптических «розеток» вокруг Солнца снова сблизилась с планетой и братья снова сравнили показания часов..
Поскольку комета двигалась то вдали от Солнца, то вблизи него, её скорость сильно менялась становясь весьма значительной, когда она летела к Солнцу, а в удаленнии, её минимальная скорость становилась равной планетной. Следовательно, часы брата, «кометного путешественника» должны отставать. Его время замедлилось по ряду причин:
Первая, он двигался с большой скоростью будучи около Солнца, причём его скорость была намного больше, чем скорость движения планеты по орбите.
Вторая, он некоторое время находился вблизи Солнца, а там, возле массивного тяготеющего тела время тоже замедляется. Время в области низкого гравитационного потенциала замедляется по сравнению со свободным от гравитации пространством.
Так что, совершенно очевидно, что часы путешественника отстанут от планетных, ибо время для него текло замедленно.
В чём же парадокс?
Парадокс в том, что оба брата свободно падали в гравитационном поле Солнца: Один вместе с планетой, другой вместе с кометой и, согласно Общему Принципу Относительности, они представляли собой две равноправные «псевдоинерциальные» системы отсчёта.  КАЖДЫЙ вправе утверждать, что время другого должно было замедлиться, ибо брат на планете, может утверждать, что не кометный брат улетел с большой скоростью, а ОН вместе с планетой отдалялся от кометы!
Мы, конечно, пренебрегаем тяготением планеты и кометы, считая их малыми.

Ещё раз, правильным ответом на вопрос о показаниях часов является тот, который дан перед «парадоксом»! Но именно поэтому и возник «парадокс» – братья находились в псевдоинерциальных системах отсчёта (если пренебречь собственным тяготением планеты и кометы),  в обеих соблюдались законы Ньютона, подтверждающие, что оба находятся в «инерциальных системах отсчёта». Ибо в свободно падающих в неком центральном поле системах отсчёта все явления свидетельствуют о том, что они ИНЕРЦИАЛЬНЫЕ! Причём роли не играет, что это поле центральное и напряжённость его меняется, а значит меняется и ускорение свободного падения. При любом свободном падении, все законы Ньютона  в падающих системах соблюдаются, независимо от ускорений, криволинейности и всех прочих отклонений от прямолинейного и равномерного движения (для внешнего наблюдателя) падающих систем.  Поэтому все законы для них инвариантны, то есть не должны претерпевать каких-либо изменений при переходе от одной системы к другой.
ПАРАДОКС!
22 Х 2017