Виброгенезис на службе геологии

«Особенности развития динамической (волновой) парадигмы недропользования. Звучание недр и индустриальная геологоразведка»

Геннадий Петрович Андреев, Михаил Икарович Микляев, Иван Иванович Дорофеев

Основные темы научной работы: Развитие научных направлений в области геологии, геодинамики и наук о Земле (физика, геология, космология), комплексная (виброгеодинамическая) интерпретации космо-геолого-геофизических данных, авторский вклад в формирование нового научного направления – вигеника, виброгеодинамика – в связи с задачами обеспечения геоэкологической безопасности недропользования и индустриальной геологоразведки.

Персоналии: http://www.mathnet.ru/rus/person/112595

НОВЫЕ ВИБРОГЕОДИНАМИЧЕСКИЕ ЗАКОНОМЕРНОСТИ – ОДНА ИЗ СЛАГАЕМЫХ В РАЗВИТИИ ДИНАМИЧЕСКОЙ «ВОЛНОВОЙ» ПАРАДИГМЫ НЕДРОПОЛЬЗОВАНИЯ

Аннотация
В работе показано – как фундаментальные физические и астрофизические явления находят своё проявление и отражение в геологических процессах и в их определяющих параметрах, таких, например, как седиментогенез, особенности поведения геохронологической шкалы и многие другие явления, те которые и являются предметом изучения геологии, виброгеодинамики, как исследовательского направления, изучающего колебательные аспекты существования геосреды и такого теоретического направления как вигеника. Полученные результаты позволяют вскрыть, показать и аналитически описать и смоделировать глубинные причины этих процессов. Это удается теоретически и разнопланово обосновать и представить относительно просто и наглядно. Например, по-новому привлекая уже давно известные фундаментальные физические законы – обнаруживая их новые «геологические следствия».

Ключевые слова: Виброгеодинамика, Вигеника, седиментогенез, колебательные аспекты геологической среды, динамическая «волновая» парадигма недропользования

NEW VIBROGEODYNAMIC REGULARITIES – ONE OF COMPOSED IN DEVELOPMENT OF THE DYNAMIC "WAVE" PARADIGM OF SUBSURFACE USE

Summary
In work it is shown – as the fundamental physical and astrophysical phenomena find the manifestation and reflection in geological processes and in their defining parameters, such, for example, as sedimentogenesis, features of behavior of a geochronological scale and many other phenomena, what are a subject of studying of geology, vibrogeodynamics as the research direction studying oscillatory aspects of existence of the geological environment and such theoretical direction as vigenik. The received results allow to open, show and analytically to describe and simulate the deep reasons of these processes. It works well theoretically and is versatile to prove and present rather simply and visually. For example, in a new way attracting known fundamental physical laws for a long time – finding their new "geological consequences".

Keywords: Vibrogeodinamika, Vigenika, sedimentogenesis, vibrational aspects of the geological environment, the dynamic "wave" paradigm subsoil


   Впервые обнаружена связь между двумя природными явлениями. Каждое из них уже давно и хорошо известно. Но, несмотря на это, оба они ранее изучались разрознено. То есть – вне функциональной (количественной) взаимосвязи друг с другом. Одно из них – это иерархия в блочно-кусковатой делимости земной коры (от небольших размеров – до тысяч километров). Другое – также иерархия, но уже в динамической области – в геологических циклах разных периодов (от коротких текущих собственных колебаний Земли – до многих млн. лет).
   Тем самым, удалось принципиально по-новому показать причинно-следственные соотношения между динамикой (цикличностью) и статикой (блочностью) геосреды.
   Первый из этих факторов представляет собой причину, а второй – следствие закономерностей, изученных в области природной виброгеодинамики.
   Образно говоря, такой результат представляет собой как бы, прослеживание в земной коре – простого универсального «закона маятника»: «каждому блоку – соответствует свое собственное колебание». Это допустимо определять, как одного из отображений законов фундаментальной физики – на примере геологических процессов.
   В наиболее общем виде открытые в ходе исследований закономерности восходят к отдельным космологическим представлениям, которые затрагиваются современными теориями физики «суперструн».

   Пространство испытывает расширение. На каждом его этапе звучит своя доминантная частота. Но её звучание не одинаково с течением времени. В прошлом она имеет более высокую частоту, чем в настоящем.

   Период звучания описывается формулой Т = То • еxp(-qt). То же самое изменение звучания, но уже через изменение частоты – отображает формула: w = wо • еxp(qt).

   Существует базовая частота wо, и в некоторые периоды времени – звучит и соответствующая и удвоенная, и утроенная частоты и другие кратно целочисленные значения. А также и – половинная, третья, четвертная и другие более мелкие целочисленные значения – производные от базовой частоты wо.

  …, 1/4wо, 1/3wо, 1/2wо, wо, 2wо, 3wо, 4wо, …
   
   Те же самые «прямые» и «обратные» последовательности можно проследить и по обратным величинам относительно wо – то есть по периодам, производным от То. Соотношение между «w»   и  «Т» известно в виде:
w = 2Пи() / Т  или Т = 2Пи() / w.
 
Важно, что текущий период Т = То / N.

   Естественно вспомнить (посмотрев выше), что номер любого рассматриваемого того или иного «уровня волнового поля» N = 8 – k / 2. Где «k» – уже рассмотренное выше волновое число.
   Далее (помня, что Т = То • еxp(–qt) и Т = То / N) находим такие моменты «t», в которые звучат различные гармоники  базовой частоты «wо». И добавив совсем простые поясняющие промежуточные выкладки:
t = [ln(T/ То)] / (–q) = [ln(То / N) • (1/ То) ] / (–q) = ln(1/N) / (–q) = (ln N) / q.

В итоге получаем:  t=tn = (ln N) / q, где N – целое.

   Оказалось что события геохронологической шкалы (шкала геологического времени, показывающая последовательность и соподчинённость этапов развития земной коры и органического мира Земли - эонов, эр, периодов, эпох, веков - эонотемы, эратемы, системы, отделы, ярусы) описываются натуральным математическим рядом.

   Продолжим наше изложение – относительно частоты w.  С течением времени базовая «исходная» частота  wо начинает порождать свои более высокочастотные гармоники. Это происходит с базовой частотой wо по мере её как бы «растяжения» – за счёт расширения пространства. Начинают возникать частоты: 2wо, 3wо, 4wо и т.д. – до любого «n».  Каждая последующая «дочерняя» частота может возникнуть только в определённом времени и месте.

   Такая заданность задаётся следующими объективными причинами. Скорость расширения пространства q «задана». Она нам известна из предыдущих исследований при сопоставлении данных развития двух макрорегионов России - Волго-Уральского и Западно-Сибирского, а также из исcледования по описанию и измерению скорости удаления от Земли её спутника - Луны. И мы можем рассчитать и знать время, когда возникнет – очередная гармоника.
   Это видно из двух предыдущих выражений:  Т = То • еxp(-qt)   и w = wо• еxp(qt).  Например, если в некоторый прошлый момент  времени t1 = 0  прозвучала некоторая частота w = wо, то частота равная 2wо – сможет зазвучать только в определённый момент времени   t2 = ln(2) / q. Общая формула для мометов времени, в которые могут звучать те или иные последующие гармоники имеет вид: tn = ln(n)/q.

   Каждый момент возникновения новой гармоники – особенный. Рождённый звук возникает – в резонансе с его порождающим «родительским» звучанием. Резонанс – это привлечение энергии. Возникает её всплеск. Он тут же откликается в земных процессах. Например, в виде смены одних режимов геологического развития – на другие. Такие переходы могут иметь и катострофические формы их реализации.
   Всё это мы и наблюдаем в базовом для этой работы примере – то есть в колебаниях базисов седиментации Волго-Уральской и Западно-Сибирского геологических макрорегионов, а также в других событиях, отражённых в особенностях геохронологической шкалы.
 
   Таким образом, возможно через «увеличительное стекло» астрофизических процессов – более внимательно рассмотреть – земные геологические явления. И наоборот. Например, опираясь на базовые данные по седиментогенезу Волго-Урала и Западной Сибири – возможно рассчитать такой астрофизический параметр как «q». И тогда возможно определённым образом обобщить результаты проделанной работы, исходя из следующего определения: «Что такое наука? – Это прогноз!».

   Но пока просто продолжим наше изложение. Например, возможно, используя   «q» – спрогнозировать на любой наперед заданный период – что и как будет происходить в земных процессах и в задаваемом ими седиментогенезе (колебания /подъём /опускания земной поверхности), как будет дальше выглядеть геохронологическая шкала на любом наперёд заданном масштабе, от геологического до социально-бытового.  Ранее это в опосредованном виде было показано на впервые полученных результатах моделирования седиментогенеза Волго-Урала и Западной Сибири, по результатам изучения которых были выявлены характерные периоды Галактических звучаний.

   В представленном выше изложении возможно видеть одно из отображений и конкретизаций – неразрывности «астро-геологических» взаимосвязей и развитие такого научного направления как "Астрогеология". Их более детальное изучение  – как резонансных явлений – позволяет вскрыть и дополнительные их особенности. В каждом последующем развитии событий – всегда есть определённая доля повторения  того, что уже происходило ранее, что наглядно видно вследствие выявленных симметрий в структуре временного гармонического инварианта.

   Итоговая модель подобных соотношений – позволяет «путешествовать» во времени – как в прямом направлении, так и в обратном. Ни много ни мало, а выявлен гармонический фрактальный генератор, являющийся инвариантом развития колебательных степеней системы материального проявленного мира, позволяющий прогнозировать события как прошлого, так и далёкого будущего.

   В результатах моделирования колебаний седиментационных базисов Волго-Уральского и Западно-Сибирского геологических макрорегионов (нефтегазоносных провинций - НГП) присутствуют признаки 5-ричности природных явлений. Для их описания оказалось достаточно 5 основных параметров. В нашем случае – это 5 базовых гармоник.
   Они аппроксимируют исходные данные в виде суммы 5 синусов и 5 косинусов - мощных гармоник, выявленных в процессе исследования седиментационных данных, описывающих поведение геологической среды на значительных территориях за значительное геологическое время в диапазоне от поверхности и вплоть до больших глубин.

   В итоге сложения это даёт сочетание 5 косинусоид этих базовых гармоник со своими амплитудами, частотами.

   Однако, получается так, что таким образом удаётся с высокой точностью описать только лишь по отдельности – каждую из НГП. Но вместе – в виде единой модели – это сделать никак не удавалось. Выходило, что соответствующие частоты в наборах модельных косинусоид для каждой НГП различались. Для каждой провинции они были строго определёнными  – имели свои значения.
   Но их никак не удавалось синхронизовать, т.е. описать с помощью «сквозного» единого набора частот.  Эта рассогласовка частот гармоник между двумя НГП –  как разница между величинами частот – имела определённое значение. Причём отношения всех соответствующих гармоник в модели для двух НГП оказались величиной постоянной.

   Это удивительное обстоятельство помогло продолжить дальнейшие построения моделирования «астрогеологических» взаимосвязей – учитывая расширение пространства, что позволило точно описать единой кривой объединённые НГП, развитие которых происходило в различные геологические периоды. Набор 5 базовых гармоник – сохраняется в течение времени.
   Он остаётся одним и тем же через галактический год. Меняются только частоты – единым образом – для всех 5 составляющих гармоник в общем процессе седиментогенеза в течение 2 галактических лет (Галактический год, период обращения Солнца и ближайших к нему звёзд вокруг центра Галактики. Обычно именно эту величину считают периодом вращения Галактики). 
   То есть частота от одного галактического года до другого – изменяется синхронно – для каждой из 5 гармоник. И это изменение – соответствует скорости расширения пространства в течение рассматриваемого периода.
   Таким образом, сначала мы получаем величину разности частот. Но мы знаем интервал времени, в течение которого это изменение произошло. Потому что амплитудно-частотным анализом и вайлет-обработкой удалось определить, что интервал времени между всеми синфазными точками развития двух НГП в течение двух соседних геологических периодов определяется величиной в 216 млн. лет.
   Вот за такой период и происходит набор в вычисленной  разнице  между частотами и этот период и определяет величину галактического года. Отсюда однозначно вычисляется величина скорости расширении пространства q.
 
   Но зная q мы теперь можем вычислить и моменты времени, в которые прозвучала каждая гармоника при своём геологическом развитии для каждой из НГП. Формулы следующие. Дифференциальное уравнение для изменения периода со временем  dT/dt = -q.  Решением этого уравнения является зависимость следующего вида. T = To exp(-qt).  Здесь Т – есть период, t – время, To = 1080 млн. лет. Тогда двух различных провинций можно записать для каждого периода из пятёрки, сопоставляя соответствующие периоды обеих НГП:

T1 = To exp(-qt1).  T2 = To exp(-qt2). 
T1/T2 = To exp(-q(t2-t1)).   
         ДЕЛТАt = t1 – t2.
 
   Для получения последующего итога напомним промежуточные результаты. Величина ДЕЛТАt = 216 млн. лет. Помним, что Т = 2Пи() / w. Где w – это частота. С учётом связи периода и частоты Т = 2Пи() / w – можем вычислить q, поскольку величины периодов и частот взаимосвязаны: T1/T2  = w2/w1. Эти величины вычислены из модельной косинусоиды для двух НГП. И тогда вычисляем значение для q= ln[(w2/w1)/To]/ДЕЛТАt.
 
   И теперь напомним, что отношение между собой всех периодов Tn=T(N)=T0/N – представляют собой отношение целых чисел. Поскольку рассматриваемые периоды – являются гармониками базового периода  To = 1080 млн. лет, то отношение:    Ti/Tj  = wj/wi – представляют собой отношения резонансных периодов и частот. Тогда мы можем вычислить времена – в которые наступают резонансы.                tn = t(N) = [ln(N)] / q. И мы можем определить все такие резонансные времена.

   Немного обобщим полученный результат с учётом взаимодействия и наложения друг с другом и между собой различных гармоник такой звучащей суперструны. Для этого вместо числа n возьмём отношение двух чисел p = l/m, соответствующим двум взаимодействующим гармоникам. Получим следующее выражение для времён резонансов tp = [ln(p)] / q = [ln(l/m)] / q.

   И дальше построим из них квадратную таблицу. В ней по осям и «Х», и «Y» – отложим значения «l»  и «m». А во внутренних ячейках этой таблицы – на пересечении соответствующих строк и столбцов – по данной формуле вычислим все моменты резонансов tp. На основе данных этой таблицы – построим график зависимости интервалов времени между соседними резонансами – от значения моментов времени этих резонансов.

   Мы можем построит такой график в значительном интервале времён. Например, от – 13 млрд. лет до + 13 млрд. лет. На таком графике величина времни «0» – соответствует текущему моменту времени, в котом мы находимся сейчас.  Этот график моделирует седиментационные процессы. Вернее их причины. Резонансы. Они представляют собой отдельные гармоники базовой частоты или периода           To = 1080 млн. лет. Видно, что эти особенности представляют собой фрактальный, то есть повторяющийся на разных масштабах один и тот же характер – «инвариант» – процесса.

   Он соответствует соотношениям между основными подразделениями геохронологической шкалы. Последовательный повтор во времени множественного набора из таких инвариантных блоков – описывает этот график развитие рассматриваемых геологических процессов. Они в таком описании наглядно проявляют свой повторяющийся фрактальный характер.
   Амплитуда внутренних составляющих такого фрактального инварианта – различна. Одни из них малы, а другие имеют большую величину. Последние соответствуют крупным подразделениям геохронологической шкалы, а первые – мелким единицам шкалы.

   Эта модель была сопоставлена с известными особенностями  геологической истории. Получено высокое совпадение – между модельным описанием конкретных седиментаций  двух НГП – с одной стороны, и последовательностью фактов в общепланетарной геологической истории с другой.

   Рассмотрим уравнение Кеплера : Т^2/r^3 = 4Пи()^2/gM. Здесь период (Т) и радиус (r) обращения планет вокруг Солнца – массой «М», g – гравитационная постоянная.

   Для начала перехода к виброгеодинамике дополнительно подчеркнём следующую особенность – не вполне явную с первого взгляда. Самое очевидное, что правая часть – постоянная. То есть и левая – тоже. Что это значит?
   Отношение  между периодом и радиусом орбиты «синхронно взаимосвязаны». Уже здесь становится возможным увидеть «начальное зерно» виброгеодинамических соотношений между периодом (Т) и размерами (L). Чтобы ещё ближе подойти к уравнениям виброгеодинамики обратим наше внимание на то, что размерный параметр (L) уже практически присутствует в последовательном ряду выражений для гравитационных взаимодействий – в следующем виде: L = 2Пи()r.

   В поисках «астро-геологических» закономерностей имеются давние и развитые традиции (библиография насчитывает многие сотни работ).
   Общеизвестный результат исследований в этом направлении  представляет собой доказанный факт влияния на земные процессы – со стороны орбитальных (астрофизических)  воздействий. Их эффективность в данной работе обосновывается дополнительно.
   Это делается на основе формулируемых виброгеодинамических представлений о строении Земли – как физического резонатора – в рамках устойчивых «космо-земных» взаимодействий.
   Особенно явны внеземные влияния – самых общих плането-орбитальных закономерностей. Последние  могут быть показаны в виде базовых принципиальных соотношений между орбитальными периодами для различных планет Cолнечной Системы и их внутренним строением.

   Для этого ещё раз вернёмся  к тому положению школьной физики, которое утверждает, что движение всех составных частей Солнечной Системы подчиняется закону Кеплера:  Т^2/r^3 = 4Пи()^2/gM.
Он выводится из общих гравитационных взаимодействий:
а = v^2/r = F/m = gM/r^2; Т = 2Пи()r/v;
Т^2 = 4Пи()^2r/a = 2Пи()L/a; L = aT^2/2Пи(). 
               
T – период орбитального движения;
r – радиус орбиты;
g – гравитационная постоянная;
М, m – массы взаимодействующих тел;
v – скорость;
а – центростремительное ускорение;
L – длина орбиты.

   Для наглядности последующих рассуждений – немного изменим используемое соотношение L = aT^2/2Пи(). Оно служит как бы «переходным мостиком» между космологией и геологией. Представим его в более развёрнутом виде. Для этого примем следующие обозначения:
T = T1 + Тау.
Тогда   L1 = (a/2)(T1)^2 + aТауT1.

   Сделанное преобразование и выделение указанных обозначений
выполнено для того, чтобы перейти из одной системы координат в другую – вспомогательную. Она очень нужна. Потому, что в ней становится возможным видеть дополнительные важные особенности изучаемых процессов.
               
   Здесь мы получаем одно очень важное аналитическое преимущество. Потому, что отсюда начинает просматриваться дополнительный физический смысл тех самых коэффициентов, которые были ранее уже выявлены эмпирически. И  указывались в исходном виде уравнения виброгеодинамики.

   Таким образом, постепенно становятся более очевидными следующие особенности – важные для более общего понимания виброгеодинамических процессов. Во-первых, это помогает отметить тождественность в соотношених между эмпирически построенными зависимостями (выведенными из седиментогенезов Волго-Уральской и Западно-Сибирской НГП) – с одной стороны, и теоретическими уравнениями плането-орбитальных движений – с другой стороны.

   Во-вторых, это  позволяет выявить дополнительные слагаемые в генезисе эмпирически исследуемых процессов осадконакопления.  Потому, что теоретические выкладки позволяют уточнить и доопределить ту скрытую суть эмпирических наблюдаемых процессов, которая раннее не просматривалась.

  Например,  становится возможным продвинуться несколько дальше – в том числе и в анализе смыслов коэффициентов «а» и «b», полученных ранее эмпирически, исходя из подхода виброгеодинамики о взаимосвязи размеров раздельностей земной коры и перидов их вибрационных режимов в уравнении виброгеодинамики                L = AT^2 + BT.
L и L1 имеют размерность длины,  T и (T1) – времени.
   Пара коэффициентов при T^2 и (T1)^2 – «0,32» и «a/2» – представляет собой выражение центростремительного ускорения (с его размерностью).
   Рассмотрим коэффициенты при значении периода Т в его первой степени. Это «aТау» и  «116». Здесь «Тау» обладает размерностью времени. В то время как скоростную размерность имеет «aТау» = v (см. выше).
   Из сделанных выкладок становится возможным впервые и конкретно оценить численные значения некоторых теоретических величин. Например, «v» = «aТау» = 0,36 м/год,  Тау = 6•10^15 с = 180 млн. лет,  «a» = 2 км/(млн. лет)^2, которые удалось также рассчитать и аналитически исходя из теоретических выкладок.

   Здесь мы можем видеть точную сопоставимость этих значений с теми периодами, которые были получены нами ранее при изучении колебаний седиментационных  базисов Волго-Уральской и Западно-Сибирской НГП –  в результате их амплитудно-частотного анализа и вейвлет-обработки.

   Рассмотрим дополнительные особенности виброгеодинамического выражения:          L = аТ^2 + bT. Напомним, что из  «L = 2Пи()r» – мы имеем «r = L/2Пи()».  Давайте немножко разберёмся подетальнее. Радиус-вектор (r) от центра Галактики до какого-либо её текущего положения на спирали «золотого сечения» выражает полученное уравнение: r = Альфа(k)T^2 + Бетта(k)Т.

   Ниже мы попытаемся показать природу параметра «k» , от которого зависит динамика развития спирали.

   Давайте посмотрим – как «работает» «k» над развитием Спирали по мере  его разворачивания.   Сначала дадим промежуточное выражение для Тау = То / N. 
   Поскольку N – целое число, то видно, что Тау представляют собой гармоники базового периода То, которые и были эмпирически выявлены в базисах осадконакопления Волго-Уральской и Западно-Сибирской НГП. В которых проявляется звучание гармоник суперструны и их взаимодействия или резонансов, отображаемых геохронологической шкалой.

   И поскольку N = 8 – k/2, то видно что Тау есть функция от k.
Здесь «Альфа»  и  «Бетта» связаны между собой. Это можно показать в определённой поясняющей последовательности. Она показывает дополнительную – скрытую взаимосвязь между составными частями уравнения. Чтобы это было нагляднее, вначале проиллюстрируем соотношение между линейными размерами (L) и радиальными (r).  Для этого «радиальное» выражение  умножим на «2Пи()».
 
Или  L = аТ^2 + bT = 2Пи()r = 2Пи()Альфа(k)T^2 + 2Пи()Бетта(k)Т.
 
Исходя из того, что  а = 2Пи()Альфа = Пи()Бетта/Тау,  получаем, что
Бетта = 2АльфаТау.
И Альфа = Бетта/(2Тау).

   Число уровней подсистем l тоже есть функция от к, поскольку оно описывается выражением l = 2k +1. Например, это позволяет очень точно описать закономерность расположения планет Солнечной системы в зависимости от их уровня в Солнечной системе, исходя из того что число уровней Солнечной Системы 2*8+1=17 или удвоенное значение по диаметру соответственно равно 34.

   Величина «a» также является функцией от k следующего вида: a = a0(Ф^k)/N.         Ф – это известное нам значение «золотого сечения». И в свою очередь  через связь «Альфа»  и  «Бетта»  - Бетта также представляет собой функцию от k.

   Таким образом, коэффициенты в уравнении виброгеодинамики являются не «эмпирическими константами» (как обычно согласующими теоретические представления с реальностью), а встроенными функциями, более детально отображающими не явные особенности виброгеодинамических закономерностей.

   Оказывается, что в колебаниях базисов седиментации Волго-Уральской и Западно-Сибирской НГП отображается период (То)– с которым наша Галактика движется вокруг некоторого центра – внешнего по отношению к ней Центра. Подобно тому, как Земля – движется вокруг Солнца.

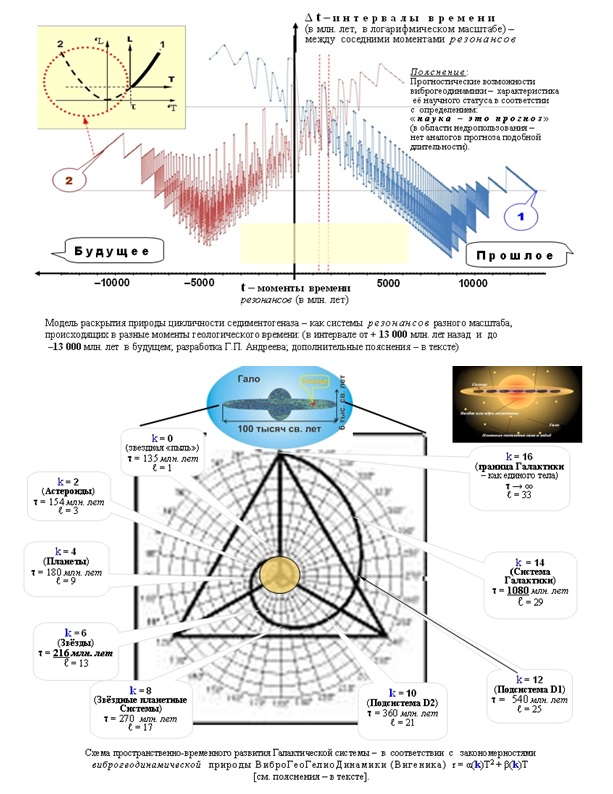
   Каждый из периодов представляет собой разные отдельные гармоники от базового периода То = 1,08 млрд. лет. И знаменуют собой определённый уровень рассматриваемой Системы (Луна-Земля-Солнце-Солнечная Система … Галактика …). Всякому такому уровню соответствует своё конкретное значение волнового числа «k».
   Для уровня астероидов – характерно k = 2. Планеты имеют k = 4. Звёзды (Солнце) отличаются k = 6. У звёздных Систем k = 8  (например, у Солнечной). Галактические системы имеют k = 14 (и наша Галактика в том числе). На уровне с k = 16 Галактику можно рассматривать по аналогии с движением Солнечной Системы по её галактической орбите. То есть Галактика на уровне k = 16 «летит» как некоторое единое тело – по своей продольно-элептической орбите с периодом То = 1,08 млрд. лет.

   Однако, продолжим наше повествование дальше. Уравнения спиралей золотого сечения для радиус-вектора пространства r и периодов T представляют из себя функции вида: r = r0*exp(Пси*Фi) - Логарифмическая спираль радиус вектора пространства r, в зависимости от угла разворота спирали Фi, с шагом, определяемым углом наклона спирали U=arctg(Пси). Хотя надо заметить, что в движении и жизни Галактики присутствует и играет свою роль для её описания не только Логарифмическая спираль радиус вектора пространства r, но также и соответствующая этой спирали разворачивающаяся Архимедова спираль вида
ra = rа0*Фa, где Фa - угол разворота Архимедовой спирали.

   Более детально это будет развёрнуто и показано в дальнейшем развитии этого повествования. Выражение для перидов T следующее:
T = T0*exp( q*t ) = T0*exp( Sigma*Фi ) - Логарифмическая спираль периодов T, в зависимости от времени, а также в зависимости от угла разворота спирали Фi, с шагом, определяемым углом наклона спирали S=arctg(Sigma).

   Тогда, исходя из вышеприведённых уравнений матрица времён резонансных событий определяется следующим выражением:
t(p=n/m)=[ln(p=n/m)]/q=Sigma*Фi/q - Архимедова спираль времени, Фi - угол разворота спирали времени.
Фi=[ln(p)]/Sigma=[ln(p=n/m)]/Sigma, где n и m - целые числа.
Фi, как и r, T, t - квантуемые, прерывные, дискретные, резонансные функции.

   И это особенно наглядно находит своё проявление в геологических процессах и в их определяющих параметрах, таких, например, как седиментационные процессы, особенности поведения геохронологической шкалы и многие и многие другие, те которые и являются предметом изучения геологии, виброгеодинамики, как исследовательского направления, изучающего колебательные аспекты проявлений в геологии и такого теоретического направления как вигеника, которые позволяют вскрыть, показать и описать глубинные причины этих процессов просто и наглядно.
   Каким образом используя знание всего о двух константах можно попробовать получить некоторые данные, описывающие то что происходит на Земле, внутри и даже вовне планеты?

   Рассмотрим маленькое переложение последовательности уравнений виброгеодинамики через взаимосвязь обнаруженных закономерностей с «золотым сечением» – «Ф» и виброгеодинамической константой – «А».
Ф = 1,618033989. Ф = [(корень квадратный из 5) + 1] / 2.
А = 1,08012345. А = корень квадратный из 7/6.

   Однако уже здесь и сейчас целесообразно подчеркнуть следующее. Эта впервые полученная константа «А» имеет  фундаментальный  характер, поскольку она согласует между собой многие величины, преимущественно связанные с величинами времени и периодов, а через них и с другими важнейшими величинами.

   Можно было бы сказать, что «Ф» в большей степени несёт в себе пространственно-статические характеристики Природы. Это как бы её «структурный квант». Вторая – «геологическая (!)» виброгеодинамическая  константа  «А» – квантует энергоструктуры Природы – по их динамике.
   Возвращаясь к уравнению виброгеодинамики возможно сказать, что его статическая L-составляющая – фокусируется в «Ф». В то время как динамическая Т-компонента  «сворачивается» – в «А». То есть «Ф» и «А» – представляют собой как бы две «свертки» виброгеодинамики – статическую и динамическую.

   Теперь давайте доопределим коэффициент «Альфа» при Т^2 в формуле:
L = f (T) = Альфа*T^2 + Бетта*T.
 
   Сделаем это в следующем виде Ф/5 = Альфа = 0,323606798. Это соответствует эмпирическому значению ~ 0,32 км/(млн. лет)^2. Последняя величина напрямую следует из анализа базисов седиментации Волго-Уральской и Западно-Сибирской НГП.

   Также скорректируем продолжительность галактического года (~216 млн.лет), выявленную из колебаний седиментационных базисов В-У и З-С НГП. Такая корректировка проводится в следующем виде: T = 2 * 100 * «А» (как ранее было указано А = 1,08012345 млн. лет).  Результат будет таким:
Т = 216,02469 или ~ 216 млн. лет.
Напомним, что Бетта = 2 * Альфа * Тау.
И пока дадим «Тау» в следующем его виде:
         Тау = 5/6 T = 180,020575 или ~ 180 млн. лет.
   Детальное обоснование выражения: Тау = 5/6 T – связано с дополнительными теоретическими рассуждениями, приведёнными ранее. Вспомним, что для Земли, волновое число которой равно 4, значение N, вычисляемое из выражения
N = 8 – k/2, равно соответственно 6.

   И тогда: Тау = T0/N = 1000*A/6 = 5/6 T,
поскольку T0 = 1000*A = 1080,12345 млн.лет, а в свою очередь
T = 2 * 100 * А = T0/5 = Т = 216,02469 млн.лет определяет период вращения Галактики.

   Подчеркнём, что значение T совпадает также с периодом Тау для звёздных уровней (или попросту для звёзд, видимо это связано с тем, что Галактика состоит  в основном всё же из звёзд, хотя здесь не лишним будет подчеркнуть, что при решении дифференциальных уравнений сферического потенциала для Галактики пришлось учитывать нечто, что находится между звёзд - об этом мы расскажем в дальнейшем, при описании полученных решений).

   Отсюда мы можем вернутся к нашим уравнениям и сказать, что все те константы (и их выражения) которые мы приводим – как раз связаны с рассмотрением и описанием представленной выше виброСистемы. Самым «малым» примером из её слагаемых является подсистема «Солнце-Земля-Луна», а другие на основе всё более общих и сложных уравнений (и волновых моделей) – продолжаются вплоть до Галактического и других уровней рассмотрения.

   Виброгеодинамика и внешняя виброСистема – рассматриваются между друг другом – в их волновом гармоничном «взаимобалансе». Он есть предмет для изучения в новом научном направлении – вигенике. Это краткое название обозначает её формальное определение (по аналогии с виброгеодинамикой) – «виброгео-гелиодинамика». На самом деле название складывалось из аббревиатуры слов «вибрация» и «генезис».
   Отсюда вигеника – это наука о естественном происхождении – генезисе природных вибраций и об их разномасштабных взаимосвязях и соотношениях – от реального времени – до геологического или – от планетарных процессов до астрофизических и наоборот.

   С помощью вигеники полученные выше общие закономерности – приобретают гораздо более  фундаментальные обоснования. Это происходит за счёт того, что для выявленных теоретических зависимостей становится возможным показать и дополнительно изучить неявные ранее или неизвестные взаимосвязи.  И обратно, с позиции виброгеодинамики – посмотреть физику процессов, которые происходят на Земле, в её недрах, вплоть до ядра, на взаимосвязь этих процессов с масштабами гораздо большими.

   И так - с помощью соотношений и взаимосвязи между виброгеодинамикой и вигеникой – как практики и теории, можно рассматривать некоторые универсальные закономерности то под «микроскопом» виброгеодинамики, то через «телескоп» вигеники. То есть можно смотреть как космические законы работают на Земле – в её геосреде. Или, наоборот, как земные виброгеодинамические закономерности – продолжаются в астрофизических.
   И это единство и взаимосвязь практики и теории особенно замечательно, позволяя понимать устройство, соподчинённость, взаимосвязь природной среды, что позволяет работать с ней более осознанно, деликатно, не нарушая её законы, а согласуясь с ними, подстраиваясь под них, с огромной благодарностью к тем кто это всё так устроил и поддерживает.

   Например, это возможно на основе различных геологических данных и с помощью проявлений самой природной виброгеодинамики. Иначе говоря, приводимые здесь вспомогательные константы помогают понимать голографичность природных виброполей: «взаимоперетекание – виброгеодинамики – в вигенику и – обратно». Вот такой единый «взаимогенез» – открывается по меньшей мере для двух и совершенно разных по масштабу явлений.

   Взаимосвязи между ними или «космо-геологические соотношения» и представляет собой для вигеники – один из её предметов изучения.
Таким образом, читатель может попытаться оказать нам определённое и посильное для него доверие. И поверить, что приводимые здесь «необъясняемые» (пока) константы – на самом деле даются как результаты гораздо более общих представлений.
   Они, образно говоря – действительно «падают с Неба». Но не в готовом виде, а в результате определенных теоретических проработок.
   А последние производятся на совсем других масштабах изучения – природных явлений и их единой волновой природы.

   Теперь, ещё раз подчеркнём важность для виброгеодинамических представлений – обоих параметров – и Т, и Тау. Поэтому ясно, что такая величина как разность между ними Дельта(Тау) – также имеет большое виброгеодинамическое значение. Это есть главная периодичность геологических процессов (по Г. Штилле), таких например, как периоды горообразования – равная 36 млн. лет. И так, теперь вычислим его значение: Дельта(Тау) = Т – Тау = 36,004115 или ~ 36 млн. лет.
   Поскольку обратные величины к периодам как мы знаем являются частотами колебаний, то становится понятным, что данная величина определяет резонансные биения между колебательными уровнями звезды и планеты. Поскольку в данном случае Тау определяет период планеты, а T - звезды.
   Через уже рассмотренную взаимосвязь между основными коэффициентами «Альфа» и «Бетта» (соответственно – при Т^2 и Т) – укажем выражение для второго из них: Бетта = 2 * Альфа * Тау = 116,5117637 или ~ 117 км/млн. лет или 11,7 см/год, представляет из себя значение скорости, определяющее многие внутриземные процессы, такие как например, скорость движения мантийных масс, флюидопотоков, движение земной коры.

   Для дальнейших пояснений введём ещё один дополнительный «поясняющий» параметр: а = 2*Пи()*Альфа = Пи()*Бетта/Тау = 2,033281479 или ~ 2 км/(млн. лет)^2. Из первой части этого соотношения видно, что оно аналитически тождественно выражению окружности. Её длина – есть «а» и радиус – Альфа. Но содержательный смысл этой формулы – в физическом его понимании – это есть ускорение.

Итак, давайте определим «волновой» радиус Rф для Земли:
2Пи()Rф = 8*Бетта*T/5 = 40 271,0682 км.
   Отсюда можем найти и такой радиус, который мог бы быть обусловлен пропорциями  «золотого сечения». Это можно сделать из выражения:
2*ПИ()*Rф/4 = 10 067,76705 км, которое определяет для Земли расстояние между её четырьмя критическими меридианами, или волновыми дольками. И соответственно «волновой» радиус будет следующим:
Rф = 6 409,33957 км.

   Здесь мы можем отметить одну характерную особенность. Она  видна, если сравнить «волновые» земные размеры – с реальными. Последние, если рассматривать их средние величины – оказываются немного меньшими.  Давайте это сделаем с земными радиусами, определяемыми разными способами. Возьмём один из них «волновой», а другой – средний и сравним их между собой:
Rф – Rcр = 6 409,33957 км – 6371 км = 38,33957 км.

   Хотя из предыдущих описаний мы помним о таких величинах как величина изменчивости средней глубины сейсмособытий в течение года, зафиксированных на Земле, коррелирующих с величиной изменчивости времени суток в течение года, определяемой опять же изменчивостью скорости вращения Земли в течение года, и наконец о весьма характерной реальной форме самого геоида Земли, являющейся далеко не сферической, что конечно же определяется теми волновыми и резонансными процессами, которые происходят как внутри Земли, так и далеко за её пределами.
 
 Геосреда существует и развивается в её своеобразном –виброгеодинамическом – двуединстве, которое связывает вибрации среды – с наиболее характерными размерами отдельных геоблоков. Отсюда открывается новая научно-познавательная возможность. Она заключается в следующем.

Надо рассматривать геологические неоднородности не обособлено, то есть не столько «сами по себе», а в качестве следствия – от усталостно-волновой деструкции породных масс. Это происходит в результате циклического развития геосреды в течение реального и геологического времени.

Подобные блочно-иерархические деструкции возникают под воздействием наиболее характерных и устойчивых природных циклов – состоящих из текущих волнообразных (колебательных) сжатий и разуплотнений. Они физически одинаково происходят в самых различных объемах земной коры. В том числе и под воздействием твердоприливного трения.

В порядке одного из практических следствий из изучаемого явления природной виброгеодинамики – определяется дополнительная задача современной геофизики. Она заключается в необходимости доизучения и доразведки не только традиционной статической картины месторождений нефти и газа (в качестве их одномоментной «фотографии), но также и их динамических изменений во времени (в виде геофизической «киносъемки» – внутренних вибраций геосреды и продуктивных нефтегазонасыщенных пластов).

Все эти представления послужат целям более совершенного управления недропользованием.
В данной связи открываются новые перспективы в обеспечении экологии и промышленной безопасности при разработке залежей УВ. Например, это актуально для создания так называемых «интеллектуальных» объектов недропользования (включая месторождения полезных ископаемых – в том числе и нефти, газа, а также подземные хранилища газа).

      Рассматриваемые виброгеодинамические явления – повсеместны.
Поэтому их изучение имеет большое практическое значение – для любых видов недропользования. Особенно для обеспечения экологии и промышленной безопасности при добыче нефти и газа (и при его подземном хранении).

Важнейшее практическое следствие выявленных закономерностей заключается в новом дополнительном обосновании – экономической и экологической необходимости в инновационной геофизике. Прежде всего, имеется в виду актуальность широкого внедрения пассивной сейсмометрии (сейсмологического мониторинга недропользования – в том числе и с целью обеспечения промышленной безопасности). Иначе говоря, виброгеодинамика представляет собой – объект исследований, а передовая геофизика – адекватный служит инструментом для изучения этого объекта.
Такая инновационная геофизика позволяет экологично и с минимальными затратами – пассивно (то есть без взрывной и вибрационной активизации и возбуждения геосреды) «прослушивать» текущую виброгеодинамику недр на месторождениях УВ и на любых других объектах недропользования. Наиболее экономично это можно делать с земной поверхности и с помощью недорогих регистрирующих сейсмостанций облегченного «ранцевого» типа.
 
Огромный научный и практический вклад в приоритетные разработки в этой области геофизики были сделаны впервые в мире многими российскими учеными – чл.-корр. А.В.Николаевым, д.т.н. И.Б.Башиловым, В.В.Аксеновым, к.ф.-м.н. А.В.Горбатиковым, д.ф.-м.н. И.Я.Чеботаревой, С.А.Михайловым, к.г-м.н. В.Е.Томилиным и мн. другими. В текущих исследованиях виброгеодинамики авторы имеют счастливую возможность получать прямые консультации и опыт сотрудничества с этими выдающими специалистами.

Через пассивно-сейсмометрическое доизучение месторождений УВ и их внутренней виброгеодинамики – налаживается и устанавливается обратная информационная связь между технологиями добычи (включая наземные установки и режимы работы скважин) – с одной стороны, и глубинной природной виброгеодинамикой – с другой стороны (включая текущие внутрипластовые процессы, в том числе и их флюидодинамику).
Подобная геофизическая связь с подземными объектами технологического воздействия – представляет собой главный принцип управления объектами любого типа. В настоящее время этот принцип практически не соблюдается в полной мере. Так как почти все традиционные методы геологоразведки имеют лишь только констатирующий характер. Поэтому они отображают не текущую динамику процессов в геосреде, а лишь её одномоментные «фотографии» – и то с заметным отставанием во времени. В то время как для современного экологического и безопасного управления добычей нефти и газа необходима непрерывная геофизическая (пассивно-сейсмометрическая) «киносъемка» всех тех динамических процессов, которые происходят на глубине – внутри месторождений УВ.

Отсюда ограниченность недропользования только лишь традиционными способами геологоразведки – снижает возможности для упреждения и профилактики аварийных ситуаций. Например, при бурении многочисленных и дорогостоящих скважин. – Традиционная технология добычи УВ «не слышит» тех предупреждений, которые непрерывно посылает нам Природа – «голосом виброгеодинамики» месторождений.

Эти «послания» могут быть эффективно зарегистрированы и «услышаны» с помощью их пассивного сейсмолокационного мониторинга и за счет применения других методов пассивно-сейсмометрического освещения текущей внутренней виброгеодинамики недр.

 Практическое применение комплекса исследований или связки «виброгеодинамика + пассивная сейсмометрия» – соответствует пониманию Экологии в самом широком и глубоком её смысле – как адекватного соотношения между Природой и воздействующими на неё Технологиями.

Подробнее фундаментальное научное и практическое значение виброгеодинамики – целесообразно представить отдельно (в дополнительном изложении. Например, под обобщающим названием: «Виброгеодинамика – научное, практическое и мировоззренческое значение в современ-ных условиях смены познавательных парадигм»).

Отдельные результаты нашей работы частично представлены в различных публикациях. Их библиография насчитывает свыше 30 работ за период свыше 20 лет. Дважды были сделаны доклады на ежегодных Международных Рождественских образовательных чтениях в г. Москве.

В настоящее время готовиться к изданию отдельная монография о виброгеодинамике и её практическом и общеобразовательном значении.
Научно-прикладное значение виброгеодинамики – в качестве нового направления исследований – приобретает в настоящее время дополнительную актуальность. Это связано с процессами, происходящими в мировом недропользовании. Например, по причине корректировки прежней статической парадигмы недропользования – на более совершенную – динамическую. В рамках последней учитываются не только традиционная «статическая картина» в распределении структурно-литологических и фильтрационно-емкостных свойств геосреды внутри месторождений УВ (их «застывшее фото»), но также и их текущие динамические изменения во времени («мерцающая» трещиноватость пластов и др. явления), что в изложении выше образно определялось в качестве «геофизического кино» о внутренней – виброгеодинамической – жизни месторождений полезных ископаемых.

Изучение виброгеодинамики в практических целях (в том числе и с помощью пассивной сейсмометрии) – позволяет более целенаправленно и точно планировать расположение дорогостоящих скважин глубокого бурения. Без этого в настоящее время оказываются нерезультативными от 10% до 50% скважин (при этом многие из них превышают по стоимости 1-2 млн. долл.). Кроме того, в рамках динамической парадигмы недропользования становится возможным эффективно осуществлять меры по энергосбережению (сохраняя до 40% электроэнергии на промыслах добычи жидких УВ). Например, за счет резонансного «подстраивания» технологических режимов добычи сырья – под текущую виброгеодинамику месторождений (в том числе под периодические сжатия и разуплотнения их геосреды, а также под «мерцающую трещиноватость» и под уточненную конфигурацию сетей дренирования залежей и под другие  особенности текущих изменений геосреды, что недоступно для изучения с помощью только традиционных средств индустриальной геологоразведки).


Литература

1. Цикличность геодинамики и газонефтеносность / Андреев Г.П., Микляев М.И., Кантемиров Ю.И., Николаева Л.Е., Полянский Н.К., Прохонов С.В. // Геодинамика нефтегазоносных бассейнов / Тезисы и Материалы Второй Международной конференции 19-21 октября 2004 гг. М.: РГУ нефти и газа имени И.М. Губкина., т. 1, C. 132-135, Москва, 2005 г., Материалы, С.68-76.

2. Волновая эволюция геоида – практические следствия в связи с газонефтеносностью, многоволновой сейсморазведкой и вибросейсмическими воздействиями / Микляев М.И., Андреев Г.П., Кантемиров Ю.Н., Астафьев Д.А., Полянский Н.К. // Проблемы геологии природного газа России и сопредельных стран: Сб.науч.тр.- М.: ВНИИГАЗ, 2005 г., (2-е изд., переработанное) 2007 г. C. 325-344. ,

3. Андреев Г.П., Микляев М.И., Аксенов В.В., Бюнау Е.К. / Системное отображение планетарной «виброгеодинамики» в геологическом строении и газонефтеносности Ямала (технологические следствия) // Фундаментальные проблемы геотектоники. Материалы XL Тектонического совещания. Том 1. – М.: ГЕОС, 2007, С. 14-17.

4. Развитие комплекса геофизических и дистанционных исследований (КГДИ). От теории до технологии. Геодинамическая антенна / Ю.Б. Баранов, Г.П. Андреев,        М.И. Микляев, В.В. Аксенов, И.В. Тищенко, Е.К. Бюнау, Ю.И. Кантемиров, А.Е. Фейгин, С.Г. Солдаткин // Фундаментальный базис новых технологий нефтяной и газовой промышленности. Теоретические и прикладные аспекты. Москва, ГЕОС, 2007, С. 29-31.

5. Виброгеодинамические основания оптимального комплекса геофизических, дистанционных, информационных технологий (КГДИ) с целью адекватного отображения единства статических и динамических свойств объектов недропользования / Г.П. Андреев, М.И. Микляев, С.Г. Солдаткин, А.А. Соколов, И.В. Тищенко, В.В. Аксенов (ООО «ВНИИГАЗ», ЗАО НПЦ «Геонефтегаз», ИФЗ РАН)// Мировые ресурсы и запасы газа и перспективные технологии их освоения (WGRR-2007): Тезисы докладов I Международной научно-практической конференции 26-27 ноября 2007 г. – М.: ВНИИГАЗ, 2007, С. 179-180.

6. Геоинформационные, Геофизические и экспериментальные исследования разномасштабной виброгеодинамики с целью совершенствования недропользования / Г.П. Андреев, Е.К. Бюнау, М.И. Микляев, И.И. Дорофеев, С.И. Солдаткин, И.В.Тищенко, В.В. Аксенов, А.Н. Камшимин (ООО «ВНИИГАЗ», ЗАО НПЦ «Геонефтегаз», ИФЗ РАН) // Мировые ресурсы и запасы газа и перспективные технологии их освоения (WGRR-2007): Тезисы докладов I Международной научно-практической конференции 26-27 ноября 2007 г. – М.: ВНИИГАЗ, 2007, С. 180-181.

7. Геннадий Андреев, Михаил Микляев, Игорь Тищенко / Виброгеодинамика и геологическое строение Ямала // Oil&Gas Journal Russia, июль-август 2007, С. 28-34.

8. Андреев Г.П. / Единство разномасштабных процессов в системе наук о Земле. Вигеника – прожектор виброгеодинамики недр // Общие и региональные проблемы тектоники и геодинамики. Материалы XLI Тектонического совещания. В 2-х томах. Том1. – М.: ГЕОС, 2008, С. 17-21.

9. И.И. Дорофеев, Г.П. Андреев, М.И. Микляев / Учебно-методическое значение системного подхода к многокомпонентному моделированию деятельности предприятий // Современное профессиональное образование и информационные технологии: тезисы докладов Международной конференции. – М.: Газпром ВНИИГАЗ, 2009, С. 70-72.

10. BELONENKO V.N., BYUNAU E.K., NIKOLASHEV V.G., MURIN V.I., ANDREEV G.P., DOROFEEV I.I., BELYAEV YU.E., KUZYANOV N.A., "MICRO-PVT SYSTEM", журнал "ПРИБОРЫ И ТЕХНИКА ЭКСПЕРИМЕНТА" , 41:2 (1998), 166-167