И. Г. Зенкевич. Не интегралом единым -8

   
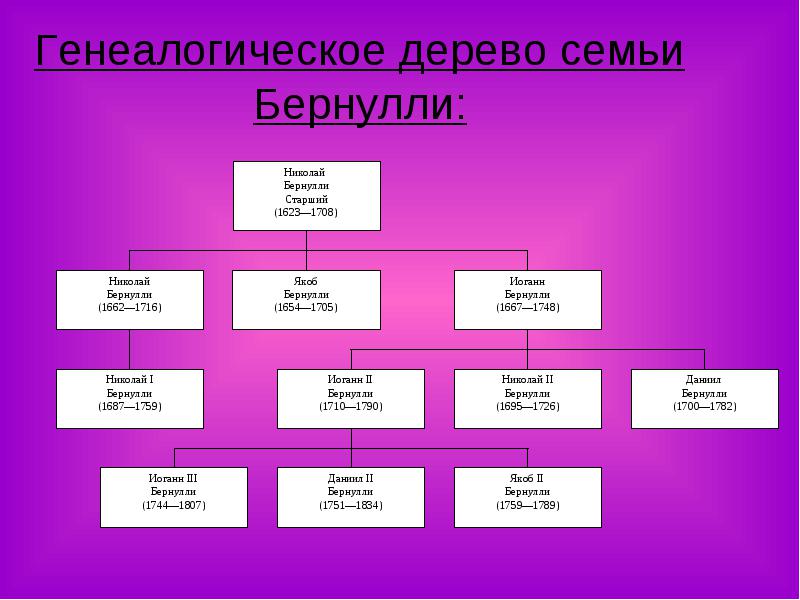
                Семейство математиков Бернулли.

   Истории наук и искусств известны семейства, в которых преемственность таланта передавалась из рода в род в течение нескольких поколений. Таково. например, музыкальное семейство Бахов со знаменитым Иоганном Себастьяном
Бахом во главе и его четырьмя сыновьями-музыкантами, его дядей, внуком и ещё тремя Бахами из того же семейства, тоже музыкантами. Или семейство французских астрономов Кассини, преемственно от  отца до правнука бывших директорами Парижской обсерватории - от её основания до времён великой революции, в течение 124 лет.
  Подобных примеров можно привести много , но едва ли найдётся семейство, которое в этом отношении не только превосходило, но даже равнялось бы со знаменитым семейством Бернулли. Из 11 членов этого семейства, занимающих кафедры, восемь приобрели себе известность математическими трудами и между
ними трое считались первоклассными математиками  своего времени.
  Кафедра математики в родном их городе Базеле в течение 105 лет  была постоянно занята одним из Бернулли, а с 1686 года, в течение почти двух веков, мы  видим одного из Бернулли профессором в Базельском университете.
  Знаменитейшие учёные общества считали честью иметь их своими членами.  Преобразованная в 1699 году Парижская академия наук избрала в ограниченное число восьми иностранных членов двоих из семейства Бернулли, и с тех пор без перерыва, в течение столетия, один из Бернулли занимал это место.
  Семейство Бернулли оставило глубокий след в истории математической науки.
  Читая биографии Бернулли, нельзя не заметить их удивительно раннее математическое развитие : все они имели первые учёные степени в возрасте 14-19 лет.
  Вот члены этого семейства.

  Я к о б  I (1654-1705) - первый выдающийся его представитель. В 17 лет имел учёную степень магистра искусства. По настоянию отца изучал богословие, но позже самостоятельно усвоил математику , вплоть до её высших разделов
( самостоятельно потому, что в Базеле не было тогда математического факультета)
  Вместе с Лейбницем принимал участие в разработке основ дифференциального и интегрального исчислений.
  В книге "Искусство предположений"(1713), сыгравшей существенную роль в истории теории вероятностей, содержится вывод известной формулы и доказательство теоремы, носящей имя Якоба Бернули.

  И о г а н н  I (1667-1748) - третий брат и ученик Якоба, продолжал развитие дифференциального и интегрального исчислений. Его именем называется одно из дифференциальных уравнений первого порядка, обобщённое линейное.

  Н и к о л а й  I - второй брат Якоба и Иоганна. Был живописцем. У него в 1687 году родился  сын - также Н и к о л а й , который занимался дифференциальными уравнениями и теорией вероятностей и был профессором математики в Падуе и Базеле. (Умер в 1759 году)

  Н и к о л а й  II (1695-1726) - старший сын Иоганна I. Профессор математики в Петербурге; здесь и умер.

  Д а н и и л  I (1700-1782) - второй сын Иоганна I. С детских лет занимался математикой под руководством отца.
  Когда отец сообщил Лейбницу, что его Даниил проявляет успехи в математике, Лейбниц выразил удовлетворение тем, что и этот сын с малых лет уже "бернулличает".
  Занимался  математикой и механикой. Ему  принадлежит определение числа е как предела... при n, стремящимся к бесконечности.
  Восемь лет работал в Петербургской академии наук, а впоследствии состоял её почётным членом.
  Вместе со своим отцом и дядей Якобом Даниил составляет тройку самых выдающихся представителей фамилии Бернулли.
  Возвращаясь из Петербурга в Швейцарию, 33-летний Даниил Бернулли встретился в почтовой карете с неизвестным человеком. Они разговорились, разговор принял учёный оборот. Спутник Даниила поинтересовался узнать имя своего собеседника. Когда же тот назвал себя - Бернулли, то неизвестный, полагая, что простой с виду молодой человек хочет над ним посмеяться и для этого выбрал громкое имя, заметил, что его самого зовут Ньютоном. Впоследствии оказалось, что это был Тран, адъютант(адъюнкт-?-КС) Французской академии наук.
  По рекомендации Даниила 19-летний Эйлер был избран адъюнктом Петербургской академии наук.

  И о г а н н  II (1710-1770) - третий сын Иоганна I.  В 22 года был доктором права. Позже стал профессором математики. Дом его , как прежде дом отца, был местом встреч всех путешествующих учёных. Друг его Мопертюи, президент Берлинской академии , скончался после продолжительной болезни в его доме.

  И о г а н н  III (1744-1807) - старший сын Иоганна II. В 14 лет получил степень магистра. Занимался математикой и астрономией. Был членом нескольких академий. Умер в Берлине, в звании королевского астронома.

  Я к о б  II (1759-1789) - третий сын Иоганна II. Автор ценных трудов по механике. Член Петербургской академии наук. Утонул, купаясь в Неве.


  Французский математик маркиз Г и л ь о м- Ф р а н с у а де Л о п и т а л ь (1661-1704) опубликовал в 1696 году "Анализ бесконечно малых" - одно из первых изложений дифференциального исчисления ( имеется русский перевод).
  Было известно, что Лопиталь пользовался уроками Иоганна I Бернулли и что многие положения его книги принадлежат Бернулли, который сразу после смерти Лопиталя заявил, что правило раскрытия неопределённости 0/0 установлено им.
 В 1955 году была опубликована ранняя переписка Лопиталя и Бернулли , и из неё обнаружилось следующее.

  В 1694 году состоялось соглашение между Лопиталем и Бернулли, по условиям которого Лопиталь выплачивал Бернулли 300 лир ежегодно, а последний был обязан выполнять следующие условия:1) работать над проблемами, предложенными Лопиталем; 2) оповещать Лопиталя обо всех открытиях; 3) не распространять и не публиковать результатов, посылаемых Лопиталю.
  Ответ Бернулли не обнаружен , но из его письма от 22 июня 1694 года известно, что он принял условия.
  Изложение теоремы и примеров в письмах Бернулли показывает, что оно совпадает с таковыми в книге Лопиталя.
  "Правило Лопиталя" , следовательно, принадлежит Иоганну Бернулли, и должно с момента обнаружения сделки именоваться именем последнего.
 
Более подробное изложение вопроса даётся в статье Д.И.Стройка. США. Журнал "Mathematics Teacher",1963, 34, стр. 257 и след.



  Думала, как прокомментировать эту публикацию... И! Счастливый случай в лице читателя (СПАСИБО!):

древо Бернулли
прячется робко в тени
древ тунеядцев)

              Хомо Либер (http://www.stihi.ru/avtor/svoboda51) 

-----------

Природа, видно, отдыхает там,
где дети - не "в пример" своим отцам...
Кто виноват? Природа или нет ?
Тогда - обед?... в умах "привет"?...

А ныне что? Добавим интернет.

Вот говорят, теперь мышленье "клипа" -
Второе поколенье, не иначе...
А яблочко не падает от липы,
От выродившей яблони и "скачет".

Какая "зелепуха" , посмотри-ка!

                КС

 
     (Может пополняться откликами)